The spectacle of the universe becomes so much the grander, so much more beautiful, the worthier of its Author, when one knows that a small number of laws, most wisely established, suffice for all movements.
Pierre Louis Maupertuis (1744)
Among the more or less general laws, the discovery of which characterize the development of physical science during the last century, the principle of Least Action is at present certainly one which, by its form and comprehensiveness, may be said to have approached most closely to the ideal aim of theoretical inquiry. Its significance, properly understood, extends, not only to mechanical processes, but also to thermal and electrodynamic problems. In all the branches of science to which it applies, it gives, not only an explanation of certain characteristics of phenomena at present encountered, but furnishes rules whereby their variations with time and space can be completely determined. It provides the answers to all questions relating to them, provided only that the necessary constants are known and the underlying external conditions appropriately chosen.
Max Planck (1909)
Table of Contents
II. Introduction to the Principle of Least Action <— You are here
VII. V. The Spiritual Source of the Least Action Principle
This is the second installment in the series on the Principle of Least Action. In the first installment, “Principle of Least Action I,” we were introduced to teleology. We learned that teleology is a reason or an explanation for something that serves as a function of its purpose, as opposed to something that serves as a function of its cause. believed to have a purpose, goal, or end they strive towards. The end purpose is called the final cause (causa finalis). We also learned that Judaism is undoubtedly teleological to the core and that the Jewish faith is based on the belief in a purposeful G‑d, who created a purposeful world. In this (second) installment, we are going to get an intuitive introduction to the principle of least action.
II. Introduction to the Principle of Least Action
1. Minimizing Action
The principle of least action is easily understandable. Say, we have a particle at point A at time T1 and at point B at time T2. The question we may want to ask is, how did the particle get from point A to point B? In other words, what was its trajectory?
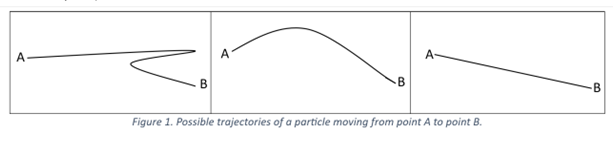
According to the recipe provided by the principle of least action, we assign a number (called “action”) to each curve and pick the curve with the smallest number—this is the actual trajectory traveled by the particle. Among the three examples given above in Figure 1, the rightmost straight line has the smallest number (action) and is, in fact, the trajectory of the particle. In the first formulation of the least action principle, it was postulated that the straight line has the least action (the smallest number associated with it). This is called the principle of least distance. Later, it was replaced by the fastest route—the trajectory that took the least time to travel and, thus, was called the least time principle (Fermat Principle). Modern formulation considers the difference between kinetic energy (the energy of motion) and potential energy (e.g., the potential energy of gravitational attraction). But more on this later. For now, we want to develop an intuition for this all-important universal principle.
Let us note that, using the least action principle, we can correctly select the trajectory the particle traveled based on the least action value associated with that trajectory. This selection is made ex post facto when we already know the particle’s position (B) at time T2. But how does a particle know where it will end up to choose the right path? Somehow, it immediately embarks on the right path a priori, as if it knew the point of destination—the final cause—which is a distinctly teleological notion.
The principle of least action states that every system evolves in time so that a certain parameter (“action,” related to energy) of the system is minimized.[1] It looks deceptively simple:
δS = 0
Here S is the parameter we are trying to minimize, called action.[2] As mentioned above, we assign a value S to all possible trajectories of a moving object (if we are talking about mechanics) and select such trajectory for which S is the smallest—it is minimized or maximized (extremized).
We will unpack the meaning of the action later. But first, let us note the teleological nature of this very important law—every physical system evolves so that a certain goal chosen a priori—extremization of action—is achieved.
2. Nature is Efficient
At the heart of the principle of least action is a surprisingly simple idea: nature is efficient. Moreover, it is maximally efficient.
Let us illustrate this principle with an everyday example.
Imagine you are entering a park, and you want to reach the opposite end. There are many paths you can take. You can go in a straight line directly towards the end of the park. You can take a roundabout way, veering off to the side before heading to the other end. You can walk around in circles for a bit before heading to the other end. Each path gets you to your destination but requires different amounts of effort. The first path is the most direct and requires the least walking. The other paths take longer and require more energy because you are moving around more.
Roughly speaking, the principle of least action says that physical systems behave like an efficient person: it “wants” to get from point A to point B in the most efficient way—that is, by using as little energy as possible. The action (the parameter we are minimizing) in this principle is a measure of the “effort” the system has to put in to follow a particular path, taking into account both its kinetic energy (energy due to motion) and its potential energy (energy due to position).
So, just like we might choose the shortest path across the park to conserve our energy, a physical system “chooses” the path that minimizes its action.
Of course, this is a simplified way to look at it. But the underlying idea is that nature takes the path of least effort—the most efficient path that minimizes action. Again, achieving this efficiency is a teleological goal chosen a priory.
This concept is intuitive to someone who believes that G‑d created the world. G‑d is perfect in every respect, including being perfectly efficient in creating the world. Therefore, His creation is also efficient (as much as it is possible within the limitations of the physical world), as it reflects the attributes of its Creator.
3. Optimization Principle
We can also view the least action principle as an optimization principle. From this point of view, the least action principle selects the most optimal path. Every living cell labors to optimize (or balance) the concentration of certain elements (for example, sodium and potassium) to achieve homeostasis. It does so by trial and error through various feedback mechanisms. As the founder of cybernetics, Norbert Wiener, famously noted, all feedback mechanisms are necessarily teleological.
Every company that sells a product tries to optimize the product’s price—the higher the price, the higher the profit. On the other hand, the higher the price, the fewer people can afford the product. What is the optimal balance so that the price is low enough to be affordable to most customers who want to buy the product but high enough to maintain a healthy profit? In economics, this balancing act is described by a demand curve. In general, markets operate by balancing demand and supply, and this is done through trial and error.
Physics also optimizes the balance of kinetic and potential energies by choosing the path for which action is minimal (or maximal—generally, extremal). However, the physical system does not need trial and error—somehow, it chooses the optimal path ab initio—from the get-go.
In the previous example, the least action principle was coached in terms of efficiency. Optimization is similar but a more general concept. If we choose to optimize the evolution of the physical system so as to maximize its energy efficiency, then that becomes the optimal path.
Optimization is always a balancing act. Cells balance the concentration of sodium and potassium; markets balance supply and demand; and physical systems balance kinetic and potential energy. However, physical systems balance it without balancing—their path is balanced from the beginning as if they know how to do it. Isn’t that amazing?
Again, let us take note of the teleological nature of the least action principle. Every physical system chooses a path to optimize certain a priori conditions—minimization (or extremization) of action. If you wondered why the first installment of this series was devoted to teleology, I hope, by now, your question has been answered.
From the theological point of view, there are no surprises here. The Prophet said:
Stand ye in the ways and see, and ask for the old paths, where the good way is, and walk therein, and yeh shall find rest for your soul.
Jeremiah 6:16
The Prophet calls on us to evaluate various paths and choose the optimal path—the “good way,” just as a particle chooses the optimal path according to the stationary action principle hinted at in the verse by the word “rest.”
Furthermore, G‑d is an absolute and perfect Being, which means that whatever G‑d does, He does optimally. No wonder, therefore, that His creations—human or inanimate—behave in a manner similar to that in which they were created—the optimal way.
Now that we have a basic understanding and an intuitive feeling for the principle of least action, we can take a deeper dive. In the next installment, we will cover the historical development of the principle of least action.
The nature is efficient
to take the shortest path.
It follows Omniscient,
Who teaches nature math.
It’s frugal, and it’s optimal
To choose the quickest route.
Off all the routes that possible,
The Action it computes.
The Action must be optimized—
Avoiding every flow,
Creator must be recognized
the Author of this law.
Endnotes:
[1] Strictly speaking, this parameter is either minimized or maximized—extremized—but most often, it is minimized, which is why this principle is often called the Least Action Principle. More on this later.
[2] Greek letter δ (“delta”) means variation. It is analogous to a derivative in calculus. When we want to find a minimum or a maximum (an extremum) of a function, we take a derivative of the function. Wherever the derivative is zero, at this point, the function is at its extremal (minimal or maximal) value. Similarly, when dealing with functionals (a function of functions), we vary them to see where the variation is zero—this picks a function that is minimal or maximal with respect to a certain parameter.

Yes … and homologous with Occam’s Razor