The spectacle of the universe becomes so much the grander, so much more beautiful, the worthier of its Author, when one knows that a small number of laws, most wisely established, suffice for all movements.
Pierre Louis Maupertuis (1744)
Among the more or less general laws, the discovery of which characterize the development of physical science during the last century, the principle of Least Action is at present certainly one which, by its form and comprehensiveness, may be said to have approached most closely to the ideal aim of theoretical inquiry. Its significance, properly understood, extends, not only to mechanical processes, but also to thermal and electrodynamic problems. In all the branches of science to which it applies, it gives, not only an explanation of certain characteristics of phenomena at present encountered, but furnishes rules whereby their variations with time and space can be completely determined. It provides the answers to all questions relating to them, provided only that the necessary constants are known and the underlying external conditions appropriately chosen.
Max Planck (1909)
Table of Contents
II. Introduction to the Principle of Least Action
III. History <— You are here
VII. V. The Spiritual Source of the Least Action Principle
This is the third installment in the series on the Principle of Least Action. In the first installment, “Principle of Least Action I,” we were introduced to teleology. We learned that teleology is a reason or an explanation for something that serves as a function of its purpose, as opposed to something that serves as a function of its cause. believed to have a purpose, goal, or end they strive towards. The end purpose is called the final cause (causa finalis). We also learned that Judaism is undoubtedly teleological to the core and that the Jewish faith is based on the belief in a purposeful G‑d, who created a purposeful world. In the second installment, we were introduced to the principle of least action. We learned that the principle of least action is a formal representation of such simple ideas as efficiency and optimization. Nature strives to emulate its Creator as best as it can. Therefore, the efficiency of nature is the manifestation of the perfection of the infinite Creator within the finite confines of the physical world. In this (third) installment, we are going to overview the history of the development of the least action principle, which will deepen our understanding of this cardinal principle of science.
III. History
The Principle of Least Action is a principle that plays a fundamental role in the formulation of classical mechanics (both Lagrangian and Hamiltonian mechanics), relativistic mechanics (both special and general relativity), electrodynamics, fluid mechanics, quantum mechanics, particle physics, quantum field theory, and string theory. It is also used in biology, economics, and other fields outside of physics. Its historical development is deeply interwoven with the progress of physics and understanding of the natural world. A brief overview of its history may help us develop a deeper intuitive understanding of this principle.
1. Antiquity

Figure 3. Euclid by Jusepe de Ribera, c. 1630–1635 (Wikipedia, Public Domain)
The earliest seeds of the idea can be found in Ancient Greece. Euclid[1] wrote in his Catoptrica[2] that, for the path of light reflecting from a mirror, the angle of incidence equals the angle of reflection,[3] which implies that the ray of light travels along the shortest path—a straight line.[4]
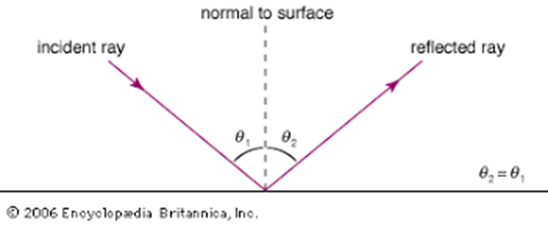
Heron of Alexandria[5] in the 1st century AD explicitly described the “law of reflection” using the concept of the “shortest path.”[6] It is an early hint of variational principles in physics.

Figure 4. 17th-century German depiction of Heron of Alexandria (Wikipedia, public domain).
From a theological point of view, choosing the right path—dereḥ ha-yashar (“the straight path”) is a religious imperative. For example, we find in Proverbs:
In all thy ways acknowledge Him, and He will straighten (yasher) thy paths.
Proverbs 3:6
We also find this imperative in the Psalms:
Teach me your way, Lord; lead me in a straight path…
Psalms 27:11
When prophesizing about the return of the exiles during the final redemption, Jeremiah writes:
I will cause them to walk by rivers of waters, in a straight path wherein they shall not stumble…
Jeremiah 31:9
Lurianic Kabbalah teaches that after the primordial contractions (Tzimtzum)—the initial concealment of the divine light Ohr Ain Sof—creating an empty space (halal) for the world, G‑d sent a ray of the divine light into the empty space. This ray of light is called in Kabbalah, the kav ([straight] line). Is it any wonder that the world created by this straight-line kav behaves similarly by choosing the straight light as the preferred trajectory of motion?
2. Renaissance
(a) Fermat Principle

Figure 5. A portrait of Pierre de Fermat by an unknown author, 17 c (public domain, Wikipedia)
The principle of least distance works well in a special case, when light travels through a single medium. However, when light traverses two or more media, such air and water, it no longer travels in a straight line—the principle of least distance no longer works in this general case. In 1662, French mathematician Pierre de Fermat proposed the “Principle of Least Time” for light propagation, now known in optics as Fermat’s principle. He suggested that light travels between two points along the path that requires the least time. He was preceded in this by Gottfried Leibniz.[7] To calculate the path of light propagating through two media one needs to calculate the times of lite traveling in each medium separately (because light travels with different speeds in different media) and then minimize the total time, which will give the angle of refraction. The principle of least time generalizes the principle of least distance.

Figure 6. Gottfried Wilhelm Leibniz, by Christoph Bernhard Francke, 1695 (Wikipedia, public domain)
To develop an intuitive understanding of the Fermat principle, let us suppose that you like to bike to work and aim to get to your office in the shortest possible time. There are two roads to your office—one straight off-road path crossing grassy loans and patches of mud, and another is a paved road that is longer but unobstructed. Following Heron’s principle of the straight path, you would choose the off-road straight path and arrive at the office late. Following a paved albeit longer road will get you to the office quicker.
Another, and perhaps better, example was given by Richard Feynman in his Lectures. Say, a lifeguard watching swimmers on a beach notices someone drawing in the ocean. He is not going to jump immediately into the ocean but will first run along the beach before entering the water, because he knows that running on a dry surface is faster than swimming in the water. The goal is to get to a drowning person as quickly as possible—that is, minimizing the total time.[8]
Choosing a priori a path that takes minimum time, has strong teleological overtones. Richard Feynman stressed that in his famous Lectures:
The idea of causality, that it goes from one point to another, and another, and so on, is easy to understand. But the principle of least time is a completely different philosophical principle about the way nature works. Instead of saying it is a causal thing, that when we do one thing, something else happens, and so on, it says this: we set up the situation, and light decides which is the shortest time, or the extreme one, and chooses that path. But what does it do, how does it find out? Does it smell the nearby paths, and check them against each other?[9]
The Talmud tells the story of Rabbi Yehoshua meeting a young boy at a crossroads. Rabbi Yehoshua asked the boy which is the way to the city, and the boy told him of two roads—a short but long way and a long but short way. Rabbi Yehoshua first took the short but long way, which was shorter in distance but had obstacles prolonging the journey. He then understood the boy’s words. There are longer paths, which are the quickest.[10] Rabbi Schneur Zalman of Liadi chose this expression—a longer but shorter way—as his epigraph Tanya.[11]
From the point of view of Jewish law, Halachah, the principle of least time appears preferable to the principle of least distance. The Talmud discusses a situation when a priest (kohen) develops a bodily impurity (tumah) while in the Temple (Bet HaMikdash).[12] The priest is not allowed to be in the Temple while in the state of tumah (ritual impurity). Should he seek the shortest or the fastest path to exit the sacred grounds? For example, he may see two gates leading outside, one closer to him and another further away. He sees crowds entering the Temple ground from the closer gate and realizes that if he runs towards the closer gate, he will be slowed down considerably by the crowds going in the opposite direction—he’d be running against the tide. The further gate is unobstructed, with no crowds between him and that gate. Obviously, trying to minimize the time of his impermissible presence on the hollow grounds, the priest is likely to run for the further gate, because it will take less time to reach.
From the point of view of the Kabbalah, it seems fitting to generalize the principle of the shortest distance with the Fermat principle. In the spiritual hierarchy of Kabbalah, time appears “before” space. In the world of Atzilut (the highest spiritual world), the six midot (lower sefirot)— Ḥesed, Gevurah, Tiferet, Netzaḥ, Hod, and Yesod—comprise the Seder HaZemanim (the “Order of Times”)—the precursor of time.[13] Space, which emerges lower on the sefirotic tree in Malḥut of Aẓilut, inherits the same structure, where six midot form six directions (four directions of the compass plus up and down) in our three-dimensional space. Furthermore, in the metaphysics of the Chasidic philosophy of Chabad, space is identified with the present “sandwiched” between the past and the future.[14] Space, in a way, originates in time. Indeed, time is defined as change and space as the absence of change (stability, constancy). However, it is the change that is the primary, not the constancy. The creation follows the rhythm of ratzo v’shov (running and returning).[15] Consequently, constancy is an unnatural state both for spiritual and physical worlds. It follows that time is primary and space is secondary. if the principle of the shortest distance is limited to a single medium, when considering a more general multi-media case, it is only natural to look at the higher reality than space, that is, time, to seek a generalization of this principle. So, replacing the shortest distance with the shortest time may reflect the kabbalistic view that, at its spiritual source, time is a higher concept than space and, in a manner of speech, encompasses space.
(b) Variational Calculus
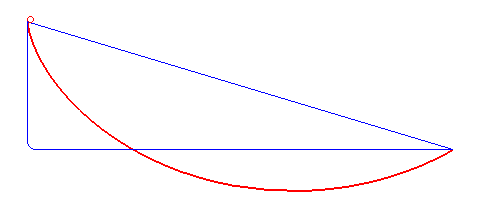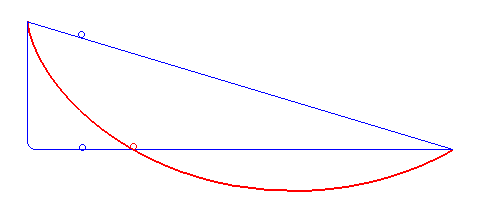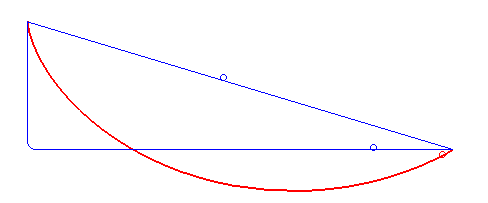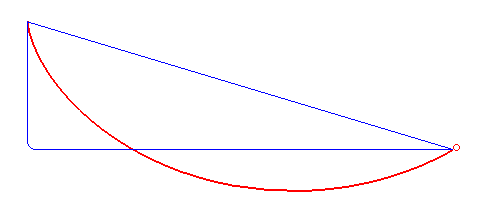
Figure 7. The curve of the fastest descent is not a straight or polygonal line (blue) but a cycloid (red). By Robert Ferréol (Public Domain, Wikimedia)

Figure 8. Johann Bernoulli by Johann Rudolf Huber, c. 1740 (Public Domain, Wikimedia)
In 1696, Johann Bernoulli[16] posed the Brachistochrone[17] problem: “What is the shape of the curve down which a bead, under the force of gravity alone, will slide (without friction) from one point to another in the least time?” The solution to this problem proposed by Johann and his brother and collaborator, Jacob Bernoulli, as well as by Isaac Newton, and others used the variational principle. They helped develop variational calculus as a mathematical discipline.[18]
(c) Principle of Least Action
In the 18th century, c. 1746, the French mathematician and physicist Pierre-Louis Moreau de Maupertuis proposed the Principle of Least Action, suggesting that nature operates in such a way as to minimize some quantity related to action. As he famously said, “Nature is thrifty in all its actions.” While Maupertuis’ formulation wasn’t fully general or entirely correct, it introduced the notion that such variational principles might describe nature.

Figure 9. Pierre Louis Moreau de Maupertuis, engraving by J. Daullé, 1741, after R. Levrac-Tournières, 1737 (Public Domain, Wikimedia)
As mentioned before, mathematically, the variational principle is expressed in a simple formula:
δS = 0
Just as in ordinary calculus, the vanishing derivative signifies the extreme (minimum or maximum) value of the function, in variational calculus, the vanishing variation signifies the extreme (minimum or maximum) value of the functional S (action).
It is interesting to note that Maupertuis did not set out to develop a new approach to physics. He developed his principle of least action, which he published in 1750 in a thin booklet titled “Essay on Cosmology,” with the sole purpose of proving the existence of G‑d. He wrote:
The laws of movement and of rest deduced from this principle being precisely the same as those observed in nature, we can admire the application of it to all phenomena. The movement of animals, the vegetative growth of plants … are only its consequences; and the spectacle of the universe becomes so much the grander, so much more beautiful, the worthier of its Author, when one knows that a small number of laws, most wisely established, suffice for all movements.[19]
This quote indicates how Maupertuis connected his principle with the idea of a grand, divinely ordered cosmos. He believed that a few simple, elegantly established laws governed all movements and phenomena in the universe, and this was a testament to the wisdom of the Creator. Although his pamphlet was met with ridicule by contemporary intellectuals, in the end, his math laid the foundation of modern physics. I believe that just as Maupertuis was justified in his math, he is justified in attributing the unity and elegance of design to the wisdom of the Creator.
The suggestion that nature operates in such a way as to minimize some quantity is teleological by definition—the physical behavior is explained by postulating a goal, a final cause.

Figure 10. Leonhard Euler By Jakob Emanuel Handmann (Public Domain, Wikimedia)
Leonhard Euler,[20] one of the most prolific mathematicians in history, greatly contributed to the development of the principle of least action by formulating the equations of motion now known as Euler-Lagrange equations. He often intertwined his scientific writings with theological reflections. He believed in the rational order of the universe and saw the hand of G‑d in its design.
In his “Letters to a German Princess,” Euler writes on various topics, touching upon the harmony of the universe and its relationship to the Creator. He wrote:
Since the fabric of the universe is most perfect and the work of a most wise Creator, nothing at all takes place in the universe in which some rule of the maximum or minimum does not appear.[21]
This passage captures Euler’s belief in a divinely ordered universe where G‑d’s wisdom is evident in the perfection and efficiency of its design.
Joseph-Louis Lagrange[22] also made foundational contributions to the calculus of variations and further developed the notion of the least action in mechanics, leading to the Lagrangian formulation of classical mechanics.

Figure 11. Joseph-Louis Lagrange (Public Domain, Wikimedia)
When we seek a path of a particle, as it evolves from the initial moment T1 to the final moment T2, it is only natural to use variational calculus. The Hebrew word shanah (“year”) is usually used as a euphemism for time.[23] Shanah is cognate with shinui (“change” or “variation”). Thus, we vary the action to determine the evolution in time.
Another way of looking at it is suggested by Maimonides, who states in his magnum opus Mishneh Torah that the right path is the middle path (dereḥ ha-nimtzoi):
The right way is the mean in each group of dispositions common to humanity; namely, that disposition which is equally distant from the two extremes in its class, not being nearer to the one than to the other.[24]
How do we achieve this middle path? In Kabbalah, the sefirotic tree has three columns—the middle column (Keter, Tiferet, Yesod, Malḥut), the right column (Ḥokhmah, Ḥesed, Netzaḥ), and the left column (Binah, Gevurah, Hod). Ideally, we are urged to pursue the middle path (or column). In reality, however, we try to find this middle path by deviating a bit to the right, every time correcting ourselves to get back to the middle but missing the mark and deviating a bit to the left, again correcting ourselves to get back to the middle, and so on. This oscillation between opposite extremes trying to achieve the middle path is a spiritual equivalent of the variational principle, whereby we vary the trajectory (the path of a particle) to find the straightest (or the fastest) path.
This is a spiritual version of the variational principle.
A theological parallel with the principle of least action is based on mimicry of G-d. There are many ways to live one’s life. Which path should we choose? The Torah teaches us that the right path is to emulate G‑d in all our our ways.[25] As it is written:
Ye shall be holy; for I, the Lord your God, am holy.
Leviticus 19:2
We should be just because G‑d is just; we should be kind because G‑d is kind, etc. In the conceptual space, where distance is measured by the degree of similarity, the imperative to emulate G‑d can be mathematically expressed as minimizing the distance that separates us from G‑d. The more G-d-like we act, the closer we are to G‑d. However, not only human beings must emulate G‑d; all nature must! Indeed, we find in Job:
…And from my flesh shall I see God.
Job 19:26
“Flesh” in this verse is a euphemism for matter or nature. We can see G‑d in nature, in the material world, because it too emulates G‑d. The Midrash says that it was as easy for God to create the world as it is for us to pronounce the letter Heh, the fifth letter of alefbet (the Hebrew alphabet), which is pronounced merely by exhaling. The Sages are telling us that creation was effortless for God. (Bereshit Rabba 3:2, 10:12), which is just an exhalation requiring no effort at all. Mimicking its Creator, nature exerts as little effort as possible in choosing the path of motion. This is a spiritual version of the least action principle.
Endnotes:
[1] Euclid, a Greek mathematician, who flourished c. 300 BCE, was the most celebrated geometer and logician of antiquity who is considered the father of geometry. He is mostly known for his treatise Elements, which established the foundations of geometry.
[2] Catoptrica, also known as Catoptrics is Euclid’s work concerns the mathematical theory of mirrors.
[3] The angle of incidence is the angle between the incoming light ray and the perpendicular line to the reflective surface. The angle of reflection is the angle between the reflected light ray and the same perpendicular line.
[4] Max Helzberger, “Optics from Euclid to Huygens,” Applied Optics, 1966, 5 (9), pp. 1383–93.
[5] Hero of Alexandria, also known as Heron of Alexandria, was a Greek mathematician and engineer, who flourished c. 60 BCE. In mathematics, he is mostly remembered for Heron’s formula for calculating the area of a triangle using only the lengths of its sides.
[6] Morris Kline, Mathematical Thought from Ancient to Modern Times. (New York: Oxford University Press, 1972) pp. 167–68.
[7] Gottfried Wilhelm (von) Leibniz (1646–1716) was a German mathematician, philosopher, and scientist. He is a very important figure in both the history of philosophy and the history of mathematics and physics.
[8] R. P. Feynman, R. B. Leighton, and M. Sands, The Feynman Lectures on Physics, Vol. II. California Institute of Technology, 1964, Chapter 26, “The Principle of Least Time.”
[9] Richard Feynman, Feynman Lectures, Lecture 26, Optics:The Principle of Least Time. (See online, https://www.feynmanlectures.caltech.edu/I_26.html#:~:text=With%20Snell’s%20theory%20we%20can,on%2C%20is%20easy%20to%20understand.)
[10] Talmud, tr. Eruvin, 53a.
[11] Rabbi Schneur Zalman of Liadi, (The Alter Rebber), Tanya, Likutei Amarim, title page.
[12] Talmud, tr. Tamid 27b.
[13] Medrash Rabba on Genesis, 20, ch. 3. See my earlier essay, “On the Nature of Time and the Age of the Universe,” (2005) (https://quantumtorah.com/on-the-nature-of-time-and-the-age-of-the-universe/).
[14] See my essays, “Space – Between Future and Past,” (June 13, 2019), (https://quantumtorah.com/space-between-future-and-past/)” and “Time as a Combination of Past and Future,” (June 30, 2023) (https://quantumtorah.com/time-as-a-combination-of-past-and-future/).
[15] “And the Chayot ran and returned as the appearance of a flash of lightning.” (Ezekiel 1:14). See my essay, “Cosmic Symphony,” QuantumTorah.com, October 30th, 2019, https://quantumtorah.com/cosmic-symphony/.
[16] Johann Bernoulli (1667–1748), a prominent Swiss mathematician, the teacher of Leonard Euler. Bernoulli made a significant contribution to calculus.
[17] Brachistochrone in Greek means the “shortest time.”
[18] The calculus of variations (or variational calculus) is a field of mathematical analysis that uses variations, which are small changes in functions and functionals, to find maxima and minima of functionals: mappings from a set of functions to the real numbers. Whereas elementary calculus is about infinitesimally small changes in the values of functions without changes in the function itself, calculus of variations is about infinitesimally small changes in the function itself, which are called variations (Richard Courant and David Hilbert, Methods of Mathematical Physics. ( New York: Interscience Publishers, Inc. 1953), Vol. I, p. 184.
[19] Pierre-Louis Moreau de Maupertuis, Essai de Cosmologie, 1750.
[20] Leonhard Euler (1707–1783), a Swiss mathematician, logician, physicist, astronomer, and engineer. He is regarded as one of the greatest mathematicians of all time. He founded the graph theory and topology. He made profound contributions to many areas of mathematics and physics, including number theory, complex analysis, calculus, mechanics, fluid dynamics, optics, and astronomy. He also contributed to music theory.
[21] Leonhard Euler, Methodus Inveniendi Lineas Curvas Maximi Minimive Proprietate Gaudentes,Lausannae & Genevae: Bousquet & Socios. 1744, 1st edition, art. 1, trans. Ivor Grattan-Guinness.
[22] Joseph-Louis Lagrange (by birth Giuseppe Luigi Lagrangia, 1736–1813) was a prominent Italian mathematician, physicist, and astronomer, who later in life became a French citizen. He made important contributions to the fields of analysis, number theory, classical and celestial mechanics.
[23] For example, Sefer Yetzirah divides the world into three domains— olam (“world,” that is space), shanah (“year,” that is time), and nefesh (“soul,” that is, spirituality). (See Sefer Yetzirah (Book of Formation), 6:4. For English translation, see Aryeh Kaplan, Sefer Yetzirah: The Book of Creation. Weiser Books, 1997.)
[24] Maimonides, Mišneh Torah, Hilḥot De’ot, Chapter 1, Halaḥa 4.
[25] Sifrei end of Ekev.