Presented at the International Torah and Science Conference in
Miami International University on December 18, 2005
Alexander Poltorak
Introduction.
This is the third in a series of articles, in which I attempt to sketch various approaches to reconciling a cosmological age of the universe currently estimated at 13.75 billion years with the Jewish tradition setting this age at less than six thousand years (5770 as of the day of this writing, to be exact).
The first article [1] tackled this problem from the point of view of Copenhagen interpretation of quantum mechanics suggesting that there were two distinct forms of existence—physical and proto-physical—and that the first conscious observers, Adam and Eve, collapsed the universal wavefunction, bringing the world from amorphous proto-physical existence into tangible physical existence. This approach leads to two distinct timelines and two legitimate ages for our universe: one, the cosmological age of proto-physical existence prior to the collapse of the wavefunction, from the Big Bang until the creation of the first human observers; and second, the much shorter age of our physical universe, from the creation of the first human observers until now.
The second article [2] in the series, approaches this problem from the point of view of the many-worlds interpretation of quantum mechanics. Not surprisingly, we again arrived at two timelines: first, the cosmological age of the multiverse from the Big Bang until the first human observers, who chose the universe in which we find ourselves based on the Anthropic principle; and the second age, from that time until now.
In this paper, we approach the age of the universe on a more fundamental level, probing the nature of time itself. Surprisingly, here too, we end up with two timelines: the static (metric) time from the Big Bang until the first humans, who set off the flow of time by construing the meaning of the self-referential construct of the universe; and the second, dynamic time (with time-flux), from that point forward.
Time
Time presents us with a riddle that has defied our understanding for millennia. We seem to be acutely aware of it but, when we try to make sense of it, we come to an impasse. Augustine of Hippo, perhaps, said it best: “Quid est ergo tempus? Si nemo ex me quærat, scio; si quærenti explicare uelim, nescio.” What then is time? If no one asks me, I know what it is. If I wish to explain it to him who asks, I know not. [3]
The fleeting sensation of time is beautifully captured in a famous rhyme attributed to Avraham ibn Ezra:
He’avar ayin
Vehe’atid adayin
Hahoveh keheref ayin
Da’ago minayin.
(Lit., The past is no more; the future is yet to come; and the present is like a blink of an eye—so whence comes worry?”) Or
The past is here no more, the future is not yet
The present lasts an eye-blink –
So whence the worry and fret?
Time plays a critical role in the existence of the universe. In fact, the very notion of existence implies temporal existence, i.e., existence in time. Nothing in the physical world exists outside of time.
Time in Jewish Thought
Time also plays a fundamental role in Judaism. Consider just a few examples:
- G‑d’s holiest name, the Tetragrammaton, Y‑H‑W‑H, is an acronym of the Hebrew root HYH (being) in three tenses—haya (was), hoveh (is), yihiyeh (will be)—past, present, and future—indicating that G‑d, for Whom past, present and future are all one, transcends time.
- The first word of the Torah is Bereshit, which is usually translated as “In the Beginning.” According to the Ramban (Nachmanides), the first words in the Torah, “Bereshit bara Elokim et hashamayim” mean that G‑d (Elokim) created (barah) the beginning (bereshit, the beginning, i.e., time) and space (shamayim).
- The very first mitzvah given to Jews in the Sinai desert, after the exodus from Egypt, was the commandment to establish a calendar by sanctifying the new moon; i.e. the commandment to keep time.
Two Aspects of Time
A close examination reveals two aspects in time. There is the metric aspect, which makes time space-like and allows us to assign every event its place on the timeline, just like any object has its coordinates in three-dimensional space. It allows us to measure the duration of the events as the distance on the timeline. In this regard, there is no difference between time and space — time behaves as a one-dimensional space. It is, therefore, easy to combine space and time into a spacetime continuum by adding the fourth dimension, time, to our familiar three-dimensional space, thereby creating a four-dimensional spacetime continuum, as was first done by Hermann Minkowski in 1907, shortly after the publication of Einstein’s Special Theory of Relativity in 1905. While Minkowski, a German mathematician of Jewish descent, may have been the first to develop the geometry of four-dimensional spacetime, appropriately called “Minkowski space,” the notion of a four-dimensional spacetime is already mentioned by one of the earliest books of Kabbalah, Sefer Yetzirah [6, 1:5, p. 44.]:
A depth of beginning
A depth of end
A depth of good
A depth of evil
A depth of above
A depth of below
A depth of east
A depth of west
A depth of north
A depth of south.
“A depth of beginning, a depth of end” represents the opposite extremes of the dimension of time. “A depth of above, a depth of below; a depth of east, a depth of west; a depth of north, a depth of south” represents three spatial dimensions. (Interestingly, Sefer Yetzirah also adds the fifth “moral” or spiritual dimension: “A depth of good, a depth of evil.”[6]) In another place, Sefer Yetzirah again speaks of the universe as a five-dimensional construct: Shanah (“year”-time) – Makom (“place”-space) – Nefesh (“soul” spirituality), i.e., time-space-spirituality.. [6]
The possibility of combining space with time and even with a “spiritual” dimension is simple: each is orthogonal to the others (i.e., independent of the other dimensions), each behaves like a mathematical space, and each possesses a metric, i.e., a geometrical structure, which allows us to measure the distance between two points in each dimension. In space, it is the spatial distance between two points; in time, it is the duration between two events; and in the “spiritual” dimension, wherein each point represents a concept or an idea and distance is the measure of the conceptual similarity (or dissimilarity) between two ideas. [7] This metric property, common to space, time, and spirituality is static in nature.
There is, however, another aspect of time that describes the intuitively familiar property of time, namely, the “flow” of time (or the time-flux), representing its passage, bringing the future close, and eventually moving it into the ever-distant past. The sense of this unceasing flow evokes the image of a flowing river. According to Heraclitus [8], time as a river never stays still; it is impossible to relive the same moment in time, just as it is impossible to step twice into the same river. Marcus Aurelius [9, Book 4] put it thus: “Time is like a river made up of the events which happen, and a violent stream; for as soon as a thing has been seen, it is carried away, and another comes in its place, and this will be carried away too.”
It is this flow that seems to divide time into past, present, and future, with time forever flowing from future into past, or, depending on your perspective, us swimming in the river of time from the past into the future. Starting with Boltzmann, physicists have been looking for the time-flux to explain this never-ceasing flow of time, with some suggesting that time-flux is a fundamental force of nature. This quality of time, however, defies mathematical description. If we ask, “what is the speed of the time flow?” the typical answer, “one second per second,” is, of course, a tautology. [4] Most attempts to answer the question involve circular reasoning.
The absolute time of Newton and the relative time of Einstein possess only metric qualities and are devoid of “flow”; hence neither possesses the arrow of time (i.e., the asymmetrical direction of the flow of time from future to past), nor the distinction between past, present, and future. And yet, both classical Newtonian mechanics, as well as relativistic mechanics of Einstein, successfully describe physical reality in their respective domains without appealing to the notion of the flow of time. Many contemporary physicists deduce from this fact that the time-flux is not real but a figment of our imagination. Others disagree. As G. J. Whitrow put it, “The history of natural philosophy is characterized by the interplay of two rival philosophies of time—one aiming at its “elimination” and the other based on the belief that it is fundamental and irreducible.”
Despite the popular misconception, Newton’s second law is a mathematical equation that describes a static function.[10] It essentially says that if we know the position and the velocity of a particle in a moment t (which is a point on a timeline T), we can calculate its position and velocity at any other point t’ on the timeline T. The second law says nothing about the flow of time, nor does it predict that the moment at the point t’ on the timeline will “come to pass.” All points on the timeline T coexist “simultaneously,” as it were, at least as far as the mathematics of it is concerned. (It is quite possible that Newton understood this, and was therefore compelled to add, as a separate axiom, the statement that “absolute, true, and mathematical time, of itself, and from its own nature flows equably without regard to anything external.” [10, Scholium I]) Alas, the axiom about time-flow added by Newton isn’t very helpful because it is essentially circular, as it begs the question, “what is ‘flow’?” which brings us back to where we started. This axiom, unfortunately, doesn’t provide a mathematical model for the flow of time.
Many have attempted to explain time as an emergent phenomenon[4], but these attempts have yet to bear fruits.
The problem goes even deeper: theoretical physics uses the language and tools of mathematics. Mathematics, however, cannot describe time, because mathematics is essentially static. This assertion may be, at first, counter-intuitive. No one will argue that all axioms “exist simultaneously,” or that all mathematical objects, say, points on a line, “exist simultaneously.” This question is not even relevant, as the time doesn’t enter the mathematics. It appears that the difficulty in describing the “flow” of time fundamentally stems from our inability to define mathematically the very concept of change. Nevertheless, we use mathematics very effectively to describe change. We use functions and differential equations to calculate change. We use graphs to plot the change of one variable in connection with the change in another variable, say to plot distance with respect to time…
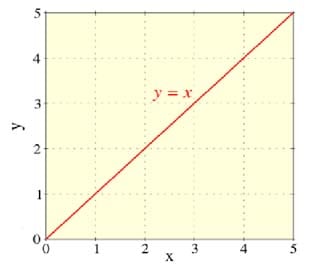
But do we really? Let’s look at the simplest graph:
All points on the X and Y axes exist simultaneously. Change is a product of our mind when we mentally “travel” from point to point on a line, contemplating one point at a time.
The only form of mathematics that uses time is algorithmic mathematics, in which steps are performed one at a time, either mentally or by a computer. Fractals are but one example of mathematical objects built algorithmically. [11] In general, the recursive function y=f(x), wherein the next value of the argument x is the value of function y calculated in a previous iteration, requires time, as each step is performed one at a time. Time, although necessary, is extrinsic to algorithmic mathematics and the latter does not explain or describe the former. Any attempts to describe time mathematically prove to be circular.
In physics, on the other hand, time plays the central role. It can be said that it is time that transforms mathematics into physics.
Indeed, all processes in nature involve time. There is no physical object or physical phenomenon that exists outside of time. Every bit of energy has its own intrinsic clock, courtesy of the de Broglie frequency associated with it: E = hν. (Where E is energy, ν is frequency and h is Planck constant) Every elementary particle has energy and, therefore, has its de Broglie frequency, which constitutes its proper clock [4]. Physics without time is unthinkable.
And yet, since physics uses the language of mathematics, which is helpless to describe time, physics too is very limited in its ability to capture the essence of time.
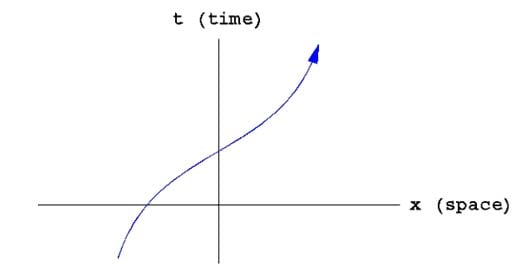
This becomes particularly apparent in light of special relativity. If one attempts to depict a world-line of a particle in the Minkowski space, the time diagram looks like this:
Every point on the world-line represents an event. All past, present and future events are depicted simultaneously on this time diagram. Luis de Broglie wrote regarding this:
“In space-time, everything which for each of us constitutes the past, the present, and the future is given in block [a four-dimensional block of reality], and the entire collection of events, successive for us, which form the existence of a material particle is represented by a line, the world-line of the particle. Each observer, as his time passes, discovers, so to speak, new slices of space-time which appear to him as successive aspects of the material world, though in reality the ensemble of events constituting space-time exist prior to his knowledge of them.”[Louis De Broglie, 1949, 114-115]
Hermann Weyl, one of the most prominent mathematicians of the 20th century, wrote [13, p. 116],
“The objective world simply is, it does not happen: Only to the gaze of my consciousness, crawling upward along the lifeline of my body, does a section of this world come to life.”
David Park similarly wrote, “our consciousness crawls along our worldline as a spark burns along a fuse.” (12, p. 113).
Moreover, special relativity did away with the absolute notions of past, present, and future, as each of these notions differ from one observer to another. As Einstein wrote to the widow of his friend Besso, “for us believing physicists, the distinction between past, present and future is only an illusion, even if a stubborn one.”
With our fundamental inability to mathematically describe—let alone explain—the concept of time, we find ourselves at an impasse. As many philosophers have noted, time-flux exists only in our minds.
Self-referential Constructs
A possible solution to the riddle of time may come unexpectedly from logic. Consider the following three aspects of time:
- The flow of time requires change. As Aristotle pointed out, “Time is a measure of change.” [16, IV:11] Moreover, “If time is a measure of change in respect of the before and after, then a necessary condition of there being time at all is the existence of change.”[17, p. 215] Unfortunately, any attempts to describe change implicitly bring time into the picture.
- For change to occur, a system must have at least two states that it can assume, as a variable must have at least two values between which it can change.
- In its bare form, time is related to causality. Ancient Romans thought that “post hoc, proctor hoc” (after means because). We know that it is a logical fallacy that is not always true, but that the inverse is always true: fact must always follow its cause. This has been the gist of the causal theory of time developed by Hans Reichenbach in 1929 [18]. This is necessary because, in order for a system to change from state A to state B, state A must have caused state B.
Let us now consider the liar’s paradox. Epimenides, a Cretan, made an immortal statement: “all Cretans are liars”. This statement is false if it’s true, and true if it’s false. Another example would be the following: consider a card on which it is written on one side, “the statement on the other side of the card is true.” On the other side, however, it says, “the statement on the other side is false.” All such paradoxes can essentially have the form, “this statement is false.”
The essential characteristic of such a statement is that it is self-referential. When we attempt to give meaning to this statement, it sets off an infinite dynamic flow: true→false→true→false, etc…
In Jewish tradition, we have a number of similar examples. Perhaps the most familiar self-referential paradox discussed widely in Jewish literature is whether the Almighty can create a stone that He cannot lift. This is not the place to discuss various approaches to this paradox among Jewish sages. Suffice it is to say, it is a typical self-referential construct that is very similar to the Liar’s paradox of antiquity.
We find an example of a self-referential construct in Gemara Nedarim [19, 69a]:
Rabbah inquired: [if upon hearing of a vow, a father or a husband said,] ‘Confirmed for you and revoked for you, and the confirmation shall not effect unless the revocation takes effect?’
We are dealing here with a situation when a father or a husband hears a woman making a vow and wants to annul this vow in a conditional form constructed by Rabbah. According to Biblical law, a father (or a husband) can revoke his daughter’s (wife’s) vow upon hearing it. Once, however, the father (husband) confirms his daughter’s (wife’s) vow, it can no longer be revoked. Here, however, the very confirmation is conditional on revocation. As a result of this self-referential construct, the vow is confirmed if revoked, and revoked if confirmed.
Consider the statement, “I am a rashah (evildoer).” In this statement, one testifies against oneself about committing a grave sin that qualifies him as a “rashah” (e.g., he admits he killed someone). If this is true, he is indeed a rashah. However, if he is a rashah, he is disqualified, according to Talmudic law, from being a witness; therefore, we don’t believe him [20, 9b]. That strikes his admission of sin and removes his disqualification as a witness, which brings us full circle back to his sinful act, etc., ad infinitum. Perhaps this vicious circle is the unstated reason that, in Talmudic law, one cannot testify against oneself in the first place.
An interesting example is discussed in Gemara Sanhedrin [20, 10a]:
Rav Yosef said: [if someone says that] a certain person sodomized him (which is a capital crime) against his will, he and another [witness] combine to testify against the sodomizer to have him put to death [for his crime]. [However, if someone says that he was sodomized] with his consent – [since, according to his own testimony,] he is a sinner, [he is ineligible to testify against the sodomizer,] for the Torah said: Do not use sinner as a witness. Rava said: a person is [considered] related to himself, and [therefore] he cannot [disqualify himself by] establishing himself a sinner.
What we have in the first part of this Gemara is a self-referential construct, wherein a person offers self-incriminating testimony against another person, so that his testimony renders him a sinner and disqualifies him as a witness. Rava decisively resolves the paradox by prohibiting self-incriminating (i.e., self-referential) testimony.
One can create many such examples, a common thread of which would be that a person’s testimony about being involved in a sinful activity disqualifies him from being a kosher witness. The Talmud resolves this conundrum by invoking the method of palginan d’dibura, i.e., “splitting the speech,” whereby we accept the part of a witness’ testimony related to another person, but do not accept the part of his testimony with respect to himself that would disqualify him as a witness altogether. In other words, the Talmud prohibits self-referential statements that cause circular reasoning.
This principle doesn’t always help. An interesting example was described in Minchat Chinuch [21]. Two witnesses come to Bet Din (Rabbinic Court) to testify that they saw the new moon. The Bet Din proclaims Rosh Chodesh (New Month) based on their testimony. Say a boy whose thirteenth birthday coincides with this declared Rosh Chodesh comes to the Bet Din and disqualifies the two witnesses as “edim zomemin” (false witnesses), stating that they had been with him at the time in another place and could not have seen the new moon. Since for a witness to be credible in a Beth Din he must be at least thirteen years old, his testimony sets off a vicious cycle: if we accept the testimony of the boy as true, thereby disqualifying original witnesses, which causes the day not to be the Rosh Chodesh, in which case the boy is not yet Bar Mitzvah, and has not reached legal majority to be accepted as a witness in court. We then must dismiss his testimony, which redeems the original witnesses and reinstates the Rosh Chodesh, thus making the boy a Bar Mitzvah, in which case we must accept his testimony, etc. ad infinitum. This is a Jewish version of classical Lair’s Paradox. As always, it involves a self-referential logical construct.
A more recent example involving set theory was described by Bertrand Russell. It is known as Russell paradox, or Russell antinomy:
It may be assumed that, for any given criterion, a set exists whose members are those objects (and only those objects) that satisfy the criterion. This assumption is disproved, however, by a set containing exactly the sets that are not members of themselves. If such a set qualifies as a member of itself, it would contradict its own definition as a set containing sets that are not members of themselves. On the other hand, if such a set is not a member of itself, it would qualify as a member of itself by the same definition. We have a paradox.
To illustrate, let us call a set “abnormal” if it is a member of itself, and “normal” otherwise. Consider, for example, the set of all triangles. That set is not itself a triangle and, therefore, is not a member of the set of all triangles. Consequently, it is a “normal” set. If we take, however, the complementary set that contains all non-triangles, that set itself is not a triangle and so should be one of its own members. Such set is “abnormal.”
Let us now consider the set of all normal sets, N. Attempting to determine whether N is normal or abnormal leads to a contradiction: if N is a normal set, it is contained in the set of normal sets (itself), and therefore is abnormal. If, on the other hand, it is abnormal, it is not contained in the set of normal sets (itself), and therefore is normal. This leads to a paradoxical conclusion that N is both normal and abnormal.
In a popular example of Russell antinomy, known as the Barber paradox, let us consider a barber who shaves men if and only if they do not shave themselves. Contemplating the question whether the barber should shave himself or not, we set off an infinite vicious cycle.
We note that in Russell antinomy, as in the Liar’s Paradox, we have a self-referential construct. There are three possible interpretations of such self-referential constructs:
(1) They are self-contradictory and must not be admitted or allowed in any mathematical theory that purports to be consistent;
(2) In any mathematical theory there are statements that cannot be proven to be either true or false by means of this theory (in essence, the Gödel theorem [24]);
(3) The paradox is resolved by the introduction of time or, alternatively, the logical sequence is what sets off the flow of time.
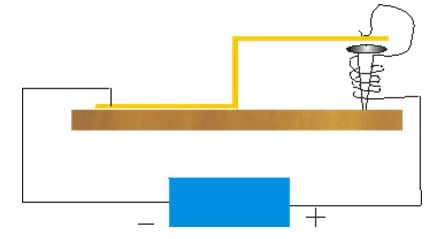
Indeed, we find in physics that such self-referential systems work very well. The simplest example would be an all-familiar electric bell. The circuitry is arranged in such a way that as soon as the circuitry is on, it turns off, and as soon as it turns off, it goes on, etc. This oscillation sets off the vibration of the hammer connected to an electromagnet, producing a ring. [25]
This can be interpreted to mean that time is necessary to break the contradiction in a self-referential system, as each logical value is assumed in a different moment in time. This brings to mind an aphorism that time is how G-d keeps things from happening all at once.[16] Or, alternatively, time-flux itself arises out of attempting to construe the meaning of a self-referential construct, such as, self-awareness.
This idea has been alluded to by others before me. Consider this quote from Paul Davies:
“Hofstadter has written of the ‘whirling vortex of self-reference’ that produces what we call consciousness and self-awareness, and I strongly believe that it is this very vortex that drives the psychological time-flux. It is for this reason I maintain that the secret of mind will only be solved when we understand the secret of time.” [4, p. 127; 20 p. 714]
This is easy to see if we introduce new terminology: a → b means that a precedes b, and that b proceeds a. The sequence: true, false, true, false can be rewritten as 1 → 0 → 1 → 0, etc. the elemental cycle of this oscillation is a pair (1, 0) representing True/False (T, F). Such a pair represents a bit of information. Consequently, this oscillation of logical values (T, F,) creates an ever-accumulating number of bits of information, which may explain the arrow of time.
Usually physicists test their theories with experiments, but this idea borders on metaphysics, and therefore cannot find support experimentally. Therefore, my reality check is to see if these thoughts can find supported in Chaza”l.
Let’s review the argument: First, time is change. As we mentioned earlier, Sefer Yetzira describes the world as existing in the three dimensions of Shana, Makom, and Nefesh—year (time), place (space) and soul (spiritual dimension). The word “shanah,” year, is etymologically related to the word “shinuy,” change. Hence, we see that the idea of time being synonymous with change is rooted in the Hebrew language of the Torah.
Second, change requires two possibilities. This too is found in Hebrew grammar as the word shinui – change – has the same letters as the word shnei – two, reflecting the notion that any change implies a transition from one state to another, for which these two state or two possibilities must exist a priori. Thus the second element of our argument is also hardwired into the Hebrew language.
Third, time requires causality. So says, for example, the Rebbe Rashab[17] in the Hemshech Samach Vav [19], as the Lubavitcher Rebbe, Rabbi Menachem Mendel Schneerson, explains in a letter expounding on the machloket (disagreement) between the Alter Rebbe and the Zidichover Rebbe on the nature of time. [19]
So far, we are on solid ground. The most audacious idea, however, is the association of time with the infinite flow of logical values – True, False – in a self-referential statement. In the Hemshech Samach Vav, Vayechulu [19], the Rebbe Rashab associates time with the kabbalistic concepts of ratzo vashov (i.e., running and returning, or to and fro), hispashtut v’histalkut (spreading and coming back), and mati velo mati (present and not present). Moti velo moti is a and not a, which brings us to our infinite sequence of True→False, etc. Thus our idea of the origin of the flow of time finds support in chassidut, in its explanation of mati velo mati and ratzo vahov as the spiritual source of time. (See [23].)
This model of time allows us to view in a new light the age of the universe. We can now separate time into two possible types of time: “static” time, which possesses metric qualities but no flow, and “dynamic” time, which has both metric qualities and the flow. Using the age-old river analogy, “static” time can be envisioned as a frozen river. One can measure the distance between fish frozen in ice as a metaphor for measuring duration between events, as “static” time retains its metric properties. Each water molecule in a frozen river has its own coordinates and maintains its relative distance, so as in frozen time, each moment has its place in the timeline, but the flow is missing. When the ice melts and the river starts flowing (while maintaining all relative distances between it molecules), this is a metaphor for the “dynamic” time.
Jewish philosophers recognized two types of time: measured time and essential time, which is called in the Guide for Perplexed shiur zman or dmut zman [23, Part 2, Ch. XIII; see also 24, p. 44], or in Sefer HaIkarim it is called zman bilti meshuar, i.e., the immeasurable time [25, Ch.2:18].
Our idea of two aspects of times neatly corresponds to the two types of time discussed by Jewish philosophers: the metric time corresponds to the immeasurable or essential time (shiur zman) and the dynamic time corresponds to the measured time (zman). On the first blush, this may seem counterintuitive. Metric time possesses metric, dt,[18] which allows us to measure distance (duration) between any two point on the timeline as an integral ∫dt. How can this correspond to the “immeasurable” time? To answer this, we need to recall that Jewish medieval philosophers were essentially neo-Aristotelians who, following Aristotle,[19] considered time to be an accident of motion. As such, time must be measured by motion (such as planetary motion, or clocks). Consequently, when there is no motion, time cannot be measured – hence it is called immeasurable time. The metric time is also immeasurable in this sense (by motion) because in metric time, which does not “flow,” there is no motion. The metric is a pure mathematical construct imposing topology on the set of events we call a timeline. Only dynamic time, which allows for motion, can be measured by moving bodies. Thus, there is no contradiction in correlating our metric time with immeasurable time (zman bilti meshuar) of Sefer HaIkarim or essential time (shiur zman or dmut zman) of Guide for the Perplexed.
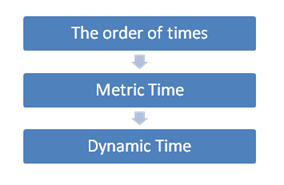
There is another complex and arcane concept of time in Judaism referred to Seder Hazmanim—the Order of Times. Medrash Rabba records the following dialog: “Rabbi Yehuda ben Shimon said, ‘It is not written, “Let there be evening” but rather, “And it was evening.” This teaches us that the order of time (seder zmanim) existed previously.’” [20, Ch. 3] This notion of seder zmanim – the order of time is further expounded in Kabbalah [21] and Chasidic philosophy [24]. Seder zmanim is a primordial form of time where there is order of event (earlier, later) but no time-flux yet. Seder zmanim is deemed to be the spiritual sourse of zman – time as it acquires the familiar property of time-flux in this world. It is somewhat similar to our notion of metric time insofar as it doesn’t have the time-flux. However, it is not clear whether the “Order of Times” has the metric topology that allows the measurement of distance between events on a time line. It seems entirely plausible that the “evolution”[20] of time proceeded as follows:
At the first stage, the primordial notion of time in its most abstract form was an ordered set of events wherein for any two events, one can say that one event preceded the other event on the timeline, i.e., the first event was “earlier” than the second event. On the second stage of development, timeline acquires metric geometry, which allows to measure the distance between two events. At this stage we not only can say that event A preceded event B but also buy how long it preceded it. Lastly, in its final stage of evolution, time acquires the property of flow, the time-flux, at which stage we call it dynamic time.
Our concept of two times also corresponds with the kabalistic notion of “lower” time, and “higher” time, lower time (corresponding to dynamic time) originating in the midot,[21] and associating with the flow of time, and higher time (corresponding to metric time) originating in the sefirot of ChaBaD (Chochmah-wisdom, Binah-understanding, Daat- Knowledge), which has metric qualities, but lacks flow.
The Age of the Universe
Our model yields two distinct timelines. The time before Adam and Eve can be classified as metric or “static” time. Adam and Eve, as the first conscious beings, set off the flow of time when they first attempted to view and understand the universe, thereby starting a new dynamic timeline.
One may ask: Adam was not from the island of Crete, so why would he be busy with the liar’s paradox? John Archibald Wheeler has answered this: “The universe through the eyes of a conscious observer looks back at itself, which brings it to a tangible existence.” [21, pp. 564-565].
The universe, in the words of late Prof. Wheeler, is the ultimate self-referential statement. According to von Neumann and Eugene Wigner only a conscious observer can collapse the wavefunction (see a detailed discussion of this in [1]). It, therefore requires a conscious being to collapse the universal wavefunction. Thus, the universe must first produce consciousness, which allows a conscious observer to look back at the universe and collapse its wavefunction; thereby, bringing it from an amorphous proto-physical existence as an abstract probability distribution into a tangible physical existence.
In our model, the universe also requires a conscious being who attempts to give meaning to this self-referential construct—the universe attempting to collapse its own wavefunction or simply to understand itself—thereby setting off the flow of time.
Thus, we again end up with two timelines: one long, cosmological timeline (currently measured as 13.75 ±0.17 billion years old [26]) and much shorter time that starts with the first humans, Adam and Eve, and which is believed, according to the Jewish tradition, to be 5770 years as of the time of this writing.
This provides another approach to resolving the contradiction between the cosmological age and the traditional Jewish age of the universe similarly to how I explained it based on a quantum mechanical model (see [1] and [2]]. In the first model [1], based on Quantum Mechanics in its traditional Copenhagen interpretation, the world before Adam and Eve existed as an abstract probability distribution described by a wavefunction. It was Adam and Eve who, looking back at the Universe, collapsed the wavefunction thereby bringing the world into its tangible existence. But the wave function comes with all its past history. Thus, when we measure today the cosmological age of the universe we find it to be approximately 13.7 billion years.
In the second model, the same results have been obtained using the contemporary many-worlds interpretation of Quantum Mechanics as well as based on my novel interpretation involving clock synchronization proposed in [2].
The Jewish Tradition, on the other hand, speaks of time from the moment this world came into actual physical existence, which happened when Adam and Eve collapsed the wavefunction (or chose one of the parallel universes in many-worlds model) some 5770 years ago.
Similarly, in our present approach, the world existed in its “frozen” form for some 13.7 billion years before the first humans came along and “unfroze” it, setting off the flow of the river of time. Once again, this new time line comes with entire history that existed before the time-flux begun so that when we measure cosmological time today, we measure the age of the universe from the time of the Big Bang, not from the moment when the time started flowing, thanks to Adam and Eve.
Conclusion
Is it coincidental that the three different approaches described my two previous papers and herein arrive at essentially the same result? I don’t think so! Of course, it is no wonder that the first two approaches yielded the same result as both were based on the same quantum mechanics albeit in its different interpretations. Why, however, did we arrive at the same result by analyzing the nature of time itself? It seems to me, there is a deep fundamental connection between quantum mechanics, the nature of time and our consciousness. As mentioned above, such undisputed authorities on quantum mechanics as von Neumann and Wigner believed that it is human consciousness that collapses the wavefunction. Likewise, we believe that it is consciousness that sets off the flow of time by attempting to construe the meaning of self-referential construct, of which consciousness attempting to understand itself is prime example. Similar sentiments have been expressed before by such thinkers as Paul Davies [4] and Douglas Hofstadter [20]. Quantum mechanics, time and consciousness all swirl around the fundamental notion of self-reference as behind all of it is the infinite, singular and omniscient Creator, who, according to the Rambam [27], knows all by knowing Himself—the ultimate self referential construct.
Bibliography:
- Alexander Poltorak, “On the Age of the Universe,” B’Ohr Hatorah (2002) vol. 13, pp.19-37
- Alexander Poltorak, “The Age of the Universe: Using the Many-Worlds Interpretation of Quantum Mechanics,” B’Ohr Hatorah (2008) vol. 18, pp. 149-168.
- Augustine of Hippo, Confessiones lib xi, cap xiv, sec 17 (ca. 400 CE).
- Paul Davies, G‑d & The New Physics. (Simon & Schuster, Inc. New York. 1984)
- Saadia Gaon
- Aryeh Kaplan, Sefer Yetzirah (Samuel Weiser, Inc., 1990)
- Aryeh Kaplan, Inner Space: Introduction to Kabbalah, Meditation and Prophecy (Moznaim, 1990)
- W. Gerson Rabinowitz and W. I. Matson, Heraclitus as Cosmologist (Philosophy Education Society Inc., 1956)
- Marcus Aurelius, The Meditations (167 CE)
- Isaac Newton, Principia Mathematica.
- Benoit Mandelbrot, The Fractal Geometry of Nature (W. H. Freeman, 1983)
- Louis De Broglie,
- Ruvin Farber and Herman Branover. B’Or HaTorah
- H. Weyl, Philosophy of Mathematics and Natural Science (Princeton University Press, Princeton, NJ, 1949).
- J.T. Fraser et al., eds., The Study of Time
- Aristotle, Physics
- Christopher John Shields, Aristotle (Routledge, New York, NY 2007)
- Hans Reichenbach, The Philosophy of Space and Time (Dover Publications, New York, NY 1958)
- Babylonian Talmud, Tr. Nedarim ArtScroll Series (Mesorah Publication, Brooklyn, NY 2000)
- Babylonian Talmud, Tr. Sanhedrin ArtScroll Series (Mesorah Publication, Brooklyn, NY 2000)
- Yosef Babad, Minchat Chinuch
- Genesis Rabba
- Rabbi Moshe Cordovero (the Ramak), Pardas Rimonim
- Douglas R. Hofstadter, G‑del, Escher, Bach: An Eternal Golden Braid (Basic Books, 1979)
- David M. Harrison, Bell Theorem (http://www.upscale.utoronto.ca/PVB/Harrison/BellsTheorem/BellsTheorem.html)
- Rebbe Rashab, Hemshech Samach Vav (Kehot, New York)
- Moses Maimonides, Guide for the Perplexed.
- Tzvi Freeman, Does Time Begin?, B’Ohr HaTorah vol.15, pp. 43
- Yosef Abo, Sefer HaIkarim
- Eliezer Zeiger, Time, B’Ohr HaTorah
- J.A. Wheeler in Isham et al., eds, Quantum Gravity (Clarendon, Oxford, 1975)
- S. H. Suyu, P. J. Marshall, M. W. Auger, S. Hilbert, R. D. Blandford, L. V. E. Koopmans, C. D. Fassnacht and T. Treu. Dissecting the Gravitational Lens B1608+656. II. Precision Measurements of the Hubble Constant, Spatial Curvature, and the Dark Energy Equation of State. The Astrophysical Journal, (2010); 711 (1)
[1] June 2010.
[2] Strictly speaking, the Cosmological time, i.e., the period from Big Bang until the present moment, is comprised of two distinct periods: (a) the proto-physical existence from the Big Bang till the first conscious observer who collapses the universal wavefunction, and (b) the physical existence from the time of the collapse of the wavefunction until the present moment. The second period, however, is less than the margin of error of the first period. Therefore, for all practical reasons, we can speak of the Cosmological period as only the first, proto-physical period.
[3] Multiverse is a term used to describe a collection of parallel universes in quantum cosmology and string theory.
[4] Another poetic translation the author heard from Rb. Shneur Zalman Stern reads as follows:
The past is not, the future aught,
The present, just a fleeting thought –
Just ask from where worried wrought?
[5] Compare this with what Paul Davies writes in G‑d and The New Physics, arguing that G-d as the Creator is only needed “to create time (strictly speaking, spacetime). [2, p. 133]
[6] The Divine emanations, Sefirot, in this context are seen as the opposite directions of each of the five dimensions – hence ten Sefirot [4, 1:5, p. 44].
[7] Ibid.
[8] If the two concepts are equivalent, they occupy the same point in conceptual space. If concept A is the negation of concept B, i.e., A = Not B, then the two concepts, A and B, are said to be are infinitely far apart. The more similar two ideas are, the closer they are position in this conceptual space. See [5].
[9] For an interesting discussion, see Olson, E.T. (2009) ―The rate of time‘s passage. Analysis 61: 3-9. van Inwagen, P. (2002) Metaphysics, 2nd Edition. Boulder, Co: Westview Press. Hudson H., Markosian N., Wasserman R., And Whitcomb D. The Rate of Passage: Reply to van Inwagen and Olson http://myweb.facstaff.wwu.edu/wasserr/papers/passage_web.pdf. In my opinion, there are two possible resolutions of this conundrum. Firstly, the question, “what is the speed of the passage of time?” is incorrect ab initio. As Aristotle already noted, time, by definition, is the rate (i.e., speed) of change. Consequently, to ask what is the rate of time is tantamount to asking “what is the rate of rate (or what is the speed of speed).” There is nothing wrong with the speed of speed for, as it is well known since the time of Newton, the speed of speed is called acceleration (i.e., the second derivative). But this is not what is being asked. The answer Olson gives is that since we cannot determine the rate of the passage of time, time does not pass. It is as absurd as to say that if a car is not accelerating, it is not moving! Secondly, according to the Special Theory of Relativity, time flows differently in different frames of reference depending on their relative speed. Therefore, one can properly say that time on an airplane flying overhead is flowing slower that time on Earth – a phenomenon known as time dilation. If fact, when we define in Special Relativity a four-dimensional vector of velocity, vi, the first three components of 4-velosity (v1,v2,v3) comprise all-too-familiar 3-velsosity of classical mechanics. The fourth component, however, v0, is calculated as v0=dx0/dτ, where τ is the proper time and x0 is time coordinate in another frame of reference. Here we have precisely the relative rate of time “flow” in one frame of reference with respect to another frame of reference!
[10] It is static diffeomorphism of a three-dimensional Euclidean space R3 into a one-dimensional Euclidean Space R1: R3 → R1, where R 1 is T and is used to describe the time dimension.
[11] Such as pressure and temperature that emerge in thermodynamics as a consequence of molecular motion.
[12] In Albert Einstein: Philosopher-Scientist, pg. 114.
[13] As we shall see later, logical contradictions of self-referential type can be “resolved” buy introduction of time, wherein the contradicting logical values take place in different moments in time. In this Talmudic example, interestingly, the analysis also takes into consideration the time element, namely, whether the statements “confirmed to you and revoked to you” take place simultaneously or consecutively (see Ran).
[14] The Torah says, “You shall not join hands with a rashah (sinner) to be a corrupt witness.” [Exodus 23;1] From this the Talmud derives that we do not use a sinner as a witness. [Sanhedrin, 9b]
[15] Rava does it by invoking a Talmudic principle of palginan dibura, i.e. splitting the statement, so that we do not accept the part of the statement with respect to the witness himself but accept the part of the testimony as it relates to another.
[16] Some say, this is an old Texas saying. A variant aphorism: “Time is how nature keeps things from happening all at once,” is alternatively attributed to A. Einstein or J. A. Wheeler.
[17] Sholom Dovber Schneersohn, the fifth Lubavitcher Rebbe (1892-1920)
[18] Metric on a set is a distance function, which defines a distance between elements of the set (in our case, a distance between the points on a timeline, i.e., duration).
[19] Although the Rambam (Maimonides) disagrees with Aristotle in one important aspect about time – according to the Rambam, time is a creation.
[20] Evolution, of course, is a temporal concept and we are admittedly guilty of circular reasoning, which is illustrative of how inextricably bound our language is with time.
[21] Midot are seven lower sefirot: chesed, gevurah, tiferet, netzach, chod, isod and malchut.


Very smart article. Like the idea that universe needs time to solve paradox of it’s self-referencial existence.
Excellent expose…..
Very brilliant writing. Thank you for this. I learned a lot, and made some interesting connections.
Two points I’d like to make for you to entertain:
1. The universe is not likely 13-14 million years old. At best, this concept is based on a look at a very small part of our universe. What we see expanding is likely just a part that is expanding. A hot air balloon could rise in a giant elevator going down; its riders would experience its descent; this would be an analogy as to how wrong the big bang theory could be. Or another analogy would be an elevator rising as viewed from the shaft doesn’t mean the building is going up as well, or that there aren’t other buildings. This is the assumption of inside-the-box thinking I dispute, despite any observed evidence to the contrary.
2. I don’t believe, like the professor quoted, that the universe could ever produce consciousness, because a.) there is no evidence, and b.) there is much evidence to the contrary… that consciousness precedes the (continuous) creation of anything that exists. Only G-d (The Infinity of Consciousness) and His likenesses, Beings, could ever create. Consciousness creates, then observes what it has created. (Of course, the observation could be faulty.) Consciousness could also create and then stop knowing what it has created, could then know some aspect of the creation, could forget that aspect, could then remember that aspect, etc. This would be a descent from full consciousness to lower states of awareness. Probably the more involved one gets in energy and space-time, the more likely one is to lose track of one’s connection to the Ultimate Source of Consciousness. But alas, that’s life. No?
I present these ideas to you only because you are much more likely than I to do something intellectual with them, assuming you see eye- to-eye with any part of them.
Thank you, it would be great if you posted your articles in a simple printable form–that way we can read it on Shabbat.
Thanks for your comment. Unfortunately, the WordPress platform where I maintain my blog does not give me any choice of format. This is the default and the only choice I have. At least, I am not aware of any way to save a PDF file. However, in light of your comment, I will research this issue further–perhaps, there is a way to do it. If you know how to do it, do tell. Shabbat Shalom!
There are some very interesting texts and papers regarding the significance of self-reference. Robert Rosen, Jewish theoretical biologist, showed that what differentiates living organisms from fabricated machines are ‘closed causal loops’ operating on a continuum. (cf. his books, ‘Life Itself’, ‘Essays on Life Itself’). Also of direct relevance is a little book by George Spencer Brown called ‘Laws of Form’ which shows that the way one goes from two-level Boolean algebra to three-level non-Boolean algebra is through the introduction of ‘time’ in association with ‘reentry into the form’. This is how one overcomes the ‘locking-up’ of paradoxical statements. The continuum of time serves as a medium. This was also explored by Francisco Varela in a paper titled ‘A Calculus of Self-Reference’ which elaborates on the ideas of Spencer Brown, particularly with regard to the logic of self-reference in the context of a calculus of ‘indications’ or ‘marking’ or ‘distinction’ between ‘this’ and ‘that’, which is the basic role of focal attention. There is also a very nice paper about ‘Self-Reference and Recursive Forms’ by LH Kauffman published in the Journal of Social and Biological Structures, 10, 53-72.
See: https://scholar.google.com/citations?view_op=view_citation&hl=en&user=H-sM-CkAAAAJ&citation_for_view=H-sM-CkAAAAJ:8xutWZnSdmoC
Last thing is to recognize the wisdom of King Solomon’s insights into the nature of time and the distinction between ‘Chronos’ (Z’man) and ‘Kairos’ (Eat) which appears in the third chapter of Qohelet. There is very deep wisdom there!
This is also central to the way that Nachmanides interprets the meaning of ‘Tohu VaVohu’… see: https://jewishphilosophyplace.com/2014/10/19/tohu-vabohu-is-tov-genesis/
This is what constitutes the ‘ouroboric’ element of consciousness as well as the relationship between the hidden realm of the quantum substratum (aka Bohm’s ‘Implicate Order’ ) which is the relational realm of the reality of possibility ( noting also that one of the names for the Shekhinah/Malkhut ) is ‘Sar HaEfshar’, the ‘Prince of Possibility’, out of which may come ‘Tov’ as an actualization that favors order, or ‘Ra’ as an actualization that favors chaos. Note that I am avoiding a blanket ethical judgment on these two forms of space-time actualization, as Nachmanides did as well–Order is not necessarily ‘Good’ and Chaos is not necessarily ‘Evil.’ It all depends on the baseline context and what is needed to address it. As the Talmudic rabbis understood quite well, without the tendency toward Ra, there would be a ‘cold death’ of excess order that would preclude novelty, creativity, and the generative. However, excess Ra leads to arbitrariness and disorder. Is this what we may call ‘Anarchy’? Not necessarily. It can also be viewed as a context that is creative and capable of solving problems and generating ‘Chidushim’ with the use of imagination. This was the distinguishing strength of Ben Zoma! However, in the context of the Pardes, Ben Zoma loses his mind and goes crazy because he saw things there that even he could not fathom, could not make sense of with the use of a vivid imagination…
By the way, spell-checker turned what I typed as ‘Eit’ into ‘Eat’ in my previous comment!
Here is the Hebrew to be clear:
זמן = Chronos (ie. metric measurable time which is ‘physical’)
עת = Kairos (ie. subjective and intersubjective flow of time which is ‘relational’)
Another reference that is relevant, I think, is a little book called ‘Laws of Form’ by George Spencer Brown which proposes and develops a ‘calculus of indication’ or ‘marking’. Without going into a lot of detail, this calculus eventually gets to the point of generating paradoxical statements whose reduced value of either ‘marked’ or ‘unmarked’ cannot be determined because if it is marked, then it is unmarked, and if it is unmarked, then it is marked. At this point, Spencer Brown introduces ‘Reentrance into the Form’ which, effectively, creates a time-dynamic that allows for oscillation between the marked and unmarked state. Interestingly, Spencer Brown shows that the mathematics of re-entrance requires the use of imaginary numbers. That is, a calculus of self-reference can be shown to require the inclusion of imaginary/complex numbers in the description of the dynamics. And the use of complex numbers is also a requirement in the equations of dynamics of quantum physics. However, classical mechanics does not have this requirement–the dynamics of Newtonian mechanics can be fully described in the domain of real numbers only. So one issue that distinguishes quantum physics from classical Newtonian physics is that the former requires the incorporation of complex numbers. What does this mean? In the context of quantum physics, Boolean (unmediated) logic is inadequate. Classical binary logic is not sufficient. One must turn to non-Boolean logic which is relational and mediated, such that it is possible to transform the contrariety of paradox into the dynamics of complementarity.