On the Age of the Universe in the Many-Worlds Interpretation of Quantum Mechanics[*]
Alexander Poltorak
Abstract
The present paper addresses the apparent discrepancy between the cosmological age of the universe, estimated at twelve to fourteen billion years, and the “biblical” age, believed in the Jewish tradition to be less than six thousand years. This paper is a sequel to my previous paper, “On the Age of the Universe,” presented at the Third Miami International Conference on Torah and Science, which aimed to resolve this contradiction from the point of view of the collapse of the wave function in the Copenhagen interpretation of Quantum Mechanics (QM). Continuing this discussion, I shall now approach the problem from the slightly different point of view of the many-worlds interpretation of QM.
This paper is a sequel to my previous paper on this subject.[1] It is currently accepted among cosmologists that the Age of the Universe from the time of the “Big Bang” until present is approximately twelve to fourteen billion years.[†] Although a rigorous and complete theory of quantum cosmology, which aught to be based on yet to be discovered quantum theory of gravitation, does not yet exist, contemporary speculative models of quantum cosmology propose that the Universe has evolved for this duration of time as a “multiverse,” i.e. collection of many parallel universes quantumly-entangled until one of this universes is chosen, according to the Antropic principle, as the only universe suitable for human habitation. According to some leading physicists, such as John Wheeler, the Universe has evolved for billions of years in its entangled state, until the first conscious observer collapses the universal wavefunction and gives our universe a tangible form. It has been proposed by Rabinowitz and Branover[2] (1990) and Poltorak[3] (2002) that this first conscious observer was Adam. In this paper I propose that the Universe has evolved in its entangled nebulous state of existence/non-existence, until Adam split the universal wavefunction (and the Universe itself) into two: one describing an existing universe and the other describing nonexistent universe, thereby giving our universe its tangible form. This approach naturally leads to two different ages: one, measured in billions of years, is the cosmological age of the evolution of the entangled universal wave function from the big bang to the present; and the other, much shorter one, is the “biblical” age of the physical universe from the time that the first human observer split (i.e., untangled) the wave function, thereby triggering our physical reality to come into being. This approach also sheds new light on an old dispute between the sages of Kabbalah regarding the sabbatical cycles, which, according to the Ari-zal, took place in spiritual “parallel” universes. In this paper, I also propose a novel interpretation of the collapse of the wavefunction as accruing due to synchronization of clocks in the frames of reference connected to the observer and the quantum-mechanical system described by the wavefunction.
Introduction
Although science and faith are based on diametrically opposite methodological principles and, consequently, may not be compared directly, when it comes to verifiable facts religion and science must agree if we are to believe that they both describe the same reality. It is particularly true for any perceived conflicts between science and Judaism. Indeed, the Sages stated that G-d looked into the Torah and created the world[4]. If the Torah served as a blueprint for the world, how can any scientific fact contradict a statement of the Torah? Thus, it behooves us to work diligently in attempting to resolve such apparent contradictions in a manner consistent with the religious tradition and experimental data, without sacrificing scientific rigor. Such attempts, in my view, should not be deemed as apologetics, but as a religious duty of any religious scientist.
Of all apparent contradictions between science and religion, the most glaring one is the question of the age of the universe. According to the Jewish tradition, the Fifth Miami International Torah and Science Conference took place in the year 5,764 from the creation of the world (2003 CE). Although I call this traditional age of the Universe a “biblical age”, it must be pointed out that the Bible does not mention explicitly when the world was created. The rabbis infer this age indirectly[5] and there are different opinions about the age of the Universe among the sages of Kabbalah.[6] That the world will exist for six thousand years is first mentioned in Babylonian Talmud, “Rav Katina says: six thousand years the world will exist…”[7] It is further elaborated by the Rishonim (early Jewish Sages) Rabbi Avraham ibn Ezra[8] and Rabbi Moshe ben Nachman (the Nachmanides)[9] in their commentaries on Pentateuch.
On the other hand, modern science places the age of the universe in the range of twelve to fourteen billion years. The latter age is supported by overwhelming experimental data, as well as by compelling theoretical considerations of contemporary cosmology. Before we approach any possible solution of this contradiction, we need to point out that, in fact, the Jewish calendar reckons the years not from the creation of the world but from the creation of the first humans – Adam and Eve. As we shall later see, this fact is highly significant. The question of the interpretation of the first six days of creation will not be addressed, as it is beyond the scope of this paper.
Copenhagen Interpretation of QM
At the Third Miami Conference, I proposed a resolution of this contradiction based on the interpretation of Quantum Mechanics (QM) given in the work of Von Neumann[10], Wigner[11] and Wheeler[12]. Essentially, this approach is based on the idea that only a conscious observer can collapse a wave function.
By way of background, the state of a quantum-mechanical system is thought to be described by a wavefunction, ψ, which satisfies the Schrödinger equation. Max Born pointed out that the square of the amplitude of the particle’s wavefunction in a given region gives the probability of finding the particle in this region of configuration space. He suggested that the wavefunction represented not a physical reality but rather our knowledge of the quantum state of an object. This approach, promulgated by the school of Niels Bohr, is known as the Copenhagen interpretation of QM, which is epistemological in nature. The wavefunction represents our knowledge of all possible quantum-mechanical states of an object. In other words, the quantum-mechanical state of a physical system is a linear superposition of all possible states of this system. According to Copenhagen interpretation, quantum mechanics does not deal with reality per se, but rather with our knowledge of reality.
The problem with this approach is that when we solve the Schrödinger equation, we obtain only a probability distribution of all possible quantum-mechanical states. When we make an experiment, however, we find the system in only one of these possible states. In other words, the time-asymmetrical process of measurement breaks the time symmetry of the Schrödinger equation. This is referred to as the Measurement Problem in QM. Measurement always reduces the world of possibilities into a single reality. Since it is expressed mathematically as a collapse of the wavefunction into a point, this problem is also referred to as a collapse of the wavefunction. Bohr suggested that it was the collision of the macro-world measurement equipment obeying the classical laws of Newton with the micro-world described by the laws of QM that led to the collapse of the wavefunction. The problem with this approach, as was pointed out by John Von Neumann, is that any macroscopic object is comprised of a finite number of microscopic building blocks – atoms and elementary particles. Since the latter must obey the laws of QM, there is no reason why macroscopic measurement equipment made of these atoms and particles should not obey the same laws. Consequently, it is not at all clear how the interaction with measurement equipment collapses the wavefunction.
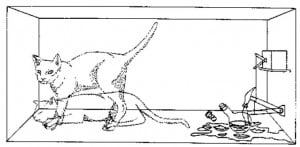
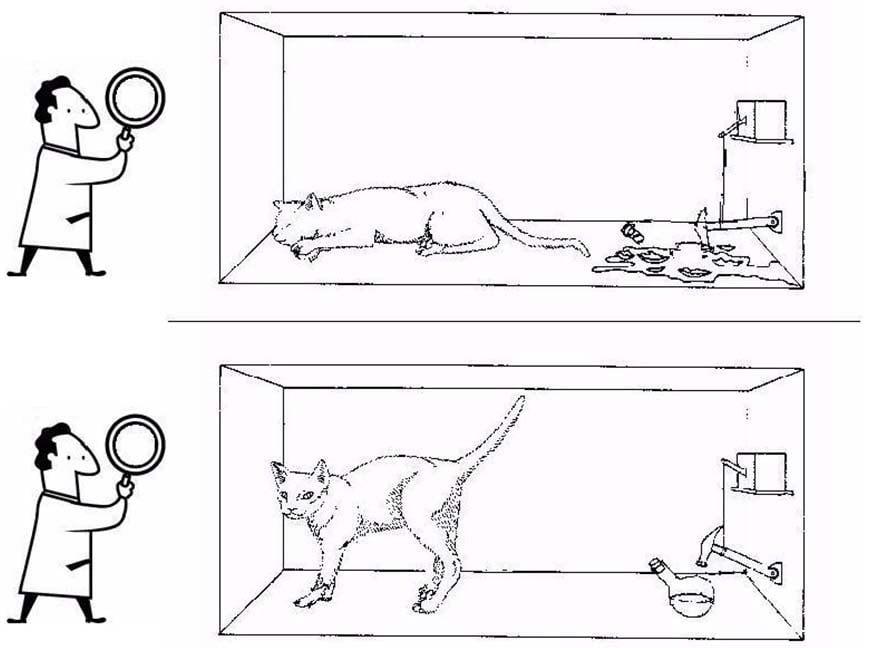
This situation leads to absurdity, as clearly demonstrated by the Schrödinger Cat gedanken experiment: an observer places a cat in a closed steel chamber, together with a Geiger tube containing some radioactive material, a hammer connected to the Geiger tube and a phial of prussic acid. From the amount of the radioactive material and its half-life, we calculate that there is a 50% chance that one atom will decay within one hour. If an atom decays, the Geiger counter is triggered, which causes the hammer to break the phial of prussic acid, which kills the cat. Prior to measurement, the quantum-mechanical state of the atom is a linear superposition of two possibilities: the decayed and the not-decayed atom. Accordingly, the state of the cat is also a linear superposition of two physical possibilities: the cat is alive and the cat is dead. In other words, before the measurement takes place, the cat is dead and alive at the same time! To be more precise, the cat is neither alive nor dead but is in an entangled state, which is a blurred combination of both possible states.
It was Von Neumann who first suggested in 1932 that, since consciousness is the only element that is time asymmetrical, it was the conscious observer that collapsed the wavefunction. Eugene Wigner and John Wheeler expanded on these ideas, which led Wheeler to replace the term observer with the term participant. Cartesian body-soul dualism is reincarnated in this approach.
Following these ideas, Rabinowitz and Branover[13] suggested that it was Adam who first collapsed the universal wavefunction, thereby participating in the creation of the world.
In my previous article on this subject[14], I suggested that there are two timelines: one reckoning billions of years from the Big Bang of fuzzy proto-physical existence before the collapse of the wavefunction by the first human observer; and the second counting years of tangible physical existence brought about by the collapse of the wavefunction by the first human observers, i.e. Adam and Eve[‡].
Many-Worlds Interpretation of QM
The approach outlined above suffers from the same difficulties as the traditional Copenhagen interpretation of QM. The collapse of the wavefunction is not part of the theory and is brought ad hoc. In this paper, we shall consider this problem from the more modern approach of the many-worlds interpretation (MWI) of QM.
 Proposed by Hugh Everett[15] in 1957 and developed by Bryce de Witt,[16] the many-worlds interpretation of QM is, perhaps, the most outlandish but yet the cleanest interpretation of QM. This theory suggests that every transition between quantum states splits the universe into multiple copies or “branches” in which all of the possible states are realized.
Proposed by Hugh Everett[15] in 1957 and developed by Bryce de Witt,[16] the many-worlds interpretation of QM is, perhaps, the most outlandish but yet the cleanest interpretation of QM. This theory suggests that every transition between quantum states splits the universe into multiple copies or “branches” in which all of the possible states are realized.
This approach, as weird as it sounds, is actually the most straightforward interpretation of the mathematical formalism of QM because it does not have to rely on an ad hoc collapse of the wavefunction, which in no way follows from the Schrödinger equation. Instead, Everett suggested that no collapse takes place, but that all of the possible states are realized in different universes. Every time-irreversible event, be that a transition between quantum-mechanical states or measurement, splits the world into as many branches as there are possible outcomes which are realized in respective branches of the universe.
Although we cannot sense the branching of the universe, Everett compared this to the criticism of the Copernicus heliocentric astronomy. We cannot sense the rotation of the Earth around the Sun either. In fact, our senses suggest the opposite – we see the Sun rising in the morning and setting in the evening. However, this is well explained by Newtonian mechanics. Similarly, QM prohibits any information exchange between various branches of the universe and, therefore, leads to this lack of awareness of the branching of the world.
A more recent variation on this theme is a parallel-universe interpretation. It differs from Everett’s original idea in two important aspects. Everett and DeWitt spoke of branching every time there was a transition between quantum states. So the world’s history looks like a huge tree, with the trunk in the past and an ever-increasing number of branches as time goes on. In the parallel-universe version, the multitude of universes exists ab initio, and a wavefunction of a quantum-mechanical system is partitioned among these parallel universes. Another difference is that, unlike the many-worlds theory that completely prohibits any communication between different branches, parallel universes can merge under certain circumstances, such as an interference experiment. For example, in a double-slit experiment, a wavefunction of a photon is partitioned between two universes: in one, the photon passes through one slit, and in another, it passes through the second slit in a completely deterministic manner. After that, due to interference, the two universes merge together producing a single tangible photon.
On this level, parallel universes remain an optional interpretation of QM, which has its followers and its skeptics. On the level of quantum cosmology, however, we are almost compelled to adopt this interpretation. Indeed, in the quantum cosmology described by the Wheeler-DeWitt equation, the universal wavefunction Ψ(h, F, S) is defined on an ensemble of all possible space-like universes, and is interpreted as a probability amplitude to find a particular manifold S with a particular geometry h and non-gravitational fields F. The Antropic principle is usually invoked to select that universe which allows for emergence of life and intelligent beings that are capable of asking the question: which particular universe we live in.
It is remarkable that the MWI or parallel universes idea boasts among its supporters such luminaries as Richard Feynman, Steven Hawking, Murray Gell-Mann, Steven Weinberg, and some of the other best theoretical physicists of the twentieth century.
It is interesting to mention that the classical Jewish sources are replete with the notion of multiple worlds and parallel universes. Consider, for example, the universes of Tohu (Chaos) and Tikun (Restoration) that coexist parallel to each other. Or the four worlds of ABYA: Atzilut (the world of Splendor), Briyah (the world of Creation), Yetzirah (the world of Formation) and Assiya (the world of Action), each of which is said to be subdivided into a myriad of parallel worlds. Needless to say, all these “universes” denote spiritual rather than physical worlds.
The most troubling aspect of the many-worlds approach is that it suggests that the observer also splits into multiple copies completely oblivious of each other – “schizophrenia with a vengeance!” I found some obscure references in the literature of Kabala that can, perhaps, be interpreted along these lines. The Zohar suggests, for example, that the three persons who came to visit Abraham in Mamre[§] where Abraham, Isaac and Jacob.[**] Here we have a “celestial copy” of Abraham visiting the “terrestrial copy” of Abraham, the two coexisting in parallel universes.
Let us now again consider the Schrödinger cat in this new light. According to the many-worlds interpretation, the decay of the radioactive atom splits the universe into two copies, thereby realizing both possibilities: decay and no decay. Accordingly, the poor cat is also split into two copies, each inhabiting one of the universes: being dead in one and alive in the other. If it would end here, it wouldn’t be so bad, but, alas, it gets worse. The observer who looks inside the box is also split into two copies, which are oblivious of one another, one observer finding a dead cat in one universe, and the other finding a live cat in the other universe.
Two Timelines
But what does all this have to do with the age of the Universe? Well, there is a curious nuance in Everett’s theory. The cat and the observer do not split into multiple copies at the same time. In fact, there are two time-irreversible events leading up to the two distinct timelines. When the atom “decays” with a probability of 50% (i.e. the state vector of the radioactive atom is the linear superposition of the two states, decayed and not decayed) the universe inside the box splits into two branches: one where the atom decays and kills the cat and the other where it does not decay and the cat is alive. This sets off one timeline. At the moment that the observer looks inside the box, he is also split into two copies: one that finds the cat dead and the other that finds the other copy of the cat alive. This second split sets off a new timeline – the one of the observer. Since the observer is conscious of neither his own branching out nor that of the cat, he thinks that his clock is synchronous with the clock inside the box. However, this copy of the universe did not exist for him before just a moment ago, while the cat has been there for a while (as long as it took from the time of radioactive decay until the time the box was opened). Consequently, it is appropriate to speak of two timelines, both of which are equally correct.
This is very similar to two time lines we spoke above when we discussed the Copenhagen interpretation of QM (see Figure 1 above).
Splitting of the World Wave-Function by the First Observer
Let us apply this logic to the question at hand. According to the contemporary cosmology, the Big Bang was set off by a random quantum fluctuation of the vacuum. Similar to the kabalistic doctrine of yesh m’ayin (i.e., creatio ex nihilo), according to the quantum field theory, before there was something, there was nothing – quantum vacuum. Although nothing usually means nothing, the Principle of Uncertainty of Heisenberg allows temporary “borrowing” of energy, which leads to the creation of virtual particles. Consequently, the physical vacuum is not quite empty; in fact, it is full of action producing and annihilating virtual particles. One such quantum fluctuation could have led to the rapid expansion of the very fabric of space-time known as the Big Bang.
Let us suppose for simplicity that the probability of such random fluctuation was 50%. This means that, at the time of this possible quantum fluctuation (t = 0), the universe branches out into two copies: one in which the fluctuation leading to the Big Bang occurs, and the other in which it doesn’t. When the first human observer (Adam) opens his eyes and looks at the universe, he is split into two copies for each of the two branches of the universe. Unfortunately, the branch of the universe in which the Big Bang never took place does not contain the planet Earth or any other conditions necessary for human habitation. Consequently, the second copy of Adam is short lived – it cannot survive even for a moment in the Big Bang singularity with infinite energy. Therefore, what we are left with is a single Adam (thank G-d!) inhabiting our branch of the universe.
In a more sophisticated version of this scenario, the initial random fluctuation of the vacuum leads to a plurality of universes – the multiverse – each having different values for fundamental physical constants. This event leads to a single universe branching into many parallel universes with different laws of physics. Only one such universe has the values of the constants just right for the emergence of conscious beings. The first such being, Adam, opens his eyes and looks at the universe, he is split into many copies, one for each of the multiple branches of the universe. Of course, the branches of the universe in which the values of physical constants are not right for the emergence of the planet Earth cannot be hospitable to other copies of the first observer. Therefore, just as in the first scenario, the other copies of Adam dot survive even for a moment in all those other (parallel) universes. Therefore, what we are still left with is a single Adam inhabiting our unique Universe.
Notwithstanding the lucky outcome of our gedanken (i.e., thought) experiment, which left us with only one copy of Adam, the two instances of branching out – one of the Universe at the initial moment t = 0, and the other of Adam at the time he first opened his eyes – do create two distinct timelines: one that flows from the moment of the Big Bang, and the other from the creation of the first human observer. Both timelines are correct and in full compliance with the many-worlds interpretation of QM.
Alternatively, from the point of view of parallel universes, at the time of the quantum fluctuation of the vacuum, the wavefunction of the world is portioned between two parallel universes: one where the Big Bang took place, and the other where it didn’t. The first human observer sets up the first interference experiment, which causes the two universes to merge together producing one physical world in which we live. Once again, we have two timelines: one that starts from the quantum fluctuation at t=0, and the other that starts at the time when Adam causes the two universes to merge together – producing our tangible physical reality.
These demonstrates how the many-worlds or parallel universes interpretations of QM resolves the controversy between the cosmological and “biblical” ages of the Universe, both of which turn out to be valid, albeit different ways of looking at the same picture.
Essentially, this result coincides with the result obtained by us in the previous paper, but without the use of the much-disputed notion of the collapse of the wavefunction.
This approach also sheds new light onto the age-old machloket (dispute) about the Sabbatical Cycles. As we noted in the previous paper[17], the dispute related to the age of the universe existed not only between science and religion but also between two major schools of the Jewish esoteric philosophy of Kabbalah. According to the ancient school of Rabbi Nehunya ben HaKanah, as explained by Rabbi Isaac of Akko, the universe existed for approximately fifteen billion years before the creation of Adam[18]. On the other hand, the Lurianic School of Kabala maintained that this took place in the spiritual rather than the physical realm.
Indeed, both opinions may not be contradictory after all. When Rabbi Nehunya ben HaKanah and Rabbi Isaac of Akko, along with the Nachmanides and other early sages of Kabala, spoke of sabbatical cycles and billions of years in pre-human history, they specifically focused on the pre-human history and therefore spoke of the first timeline – the age of the universe as originally created by G‑d, as can be clearly seen from the emphasis on using the divine years instead of the years reckoned by man. The Ari-zal further clarified the picture by pointing out that the initial phase of pre-human world history was on a different plane, which he called spiritual worlds and what contemporary physicists would call parallel universes.
Parallel Universes or Parallel Time-Lines?
As old-fashioned as it may be, but many find it hard to digest the idea that every time we look at a quantum system we are split into multiple carbon copies and that there are myriads of our clones inhabiting parallel universes completely unaware of each other. We are using here MWI only because it is one of the most popular interpretations of QM subscribed to by the majority of experts in the fields of quantum field theory and quantum cosmology.
There is another version of MWI that is much more palatable in our view. This is the Many-Histories approach of Richard Feynman.
When we study light, we use geometric optics based on Newton’s corpuscular theory of light, or wave optics based on Huygens wave theory of light. According to the Fermat principle in geometric optics, a ray of light always travels the quickest path. Waves, however, travel in all possible paths, and when they come together we add them up to compute the interference pattern.
A similar analogy exists between classical and quantum mechanics. In classical mechanics, where particles are particles, to determine a future state of the system we write a lagrangean (which is roughly the difference between potential and kinetic energy) of the system and find the extreme path that the system will follow – this is called the Principle of Least Action. In QM, where particles have waves associated with them, the waves follow all possible paths and then come together producing interference. In the 1940s, Feynman proposed to calculate all possible actions and add them together. In other words, when a QM system evolves from point A to point B (in configurational space) it travels each possible path, not just the extreme path of the least action. The method of calculating the wavefunction of a system by summing up all of its histories is called sum-over-histories approach (famous for its Feynman diagrams). Some consider this approach to be merely a clever computational aid, but others think that it actually describes the physics of the evolution of the quantum system. According to the latter view, the system does evolve over all possible paths, which is equivalent to saying that all possible states are realized in parallel universes with one exception: this approach does not require splitting the observer into multiple copies, which is fine with us. Just as geometric optics with its shortest path for the ray of light is but a narrow case of the many paths of wave optics when the light’s wavelength is sufficiently short, so is the classical mechanics with its least action path arising out of many paths of QM as its special case wherein the length of deBroglei wave of a particle is sufficiently small. It may be said that Feynman’s many-histories approach is a theory of parallel timelines – histories.
To take this concept a step further, it is our contention that the collapse of the wavefunction has to do with the synchronization of clocks in two reference frames, not unlike in the special theory of relativity. One of the main paradigm shifts of relativity is the realization that there is no absolute time: events, which are simultaneous in one reference frame, may not be simultaneous in another. Before we can compare measurements in two reference frames moving relative to each other we need to synchronize the clocks. It seems to us that a similar situation occurs in QM.
We call this approach time-relativistic interpretation of QM. By time-relativistic interpretation of QM we do not mean the standard special relativistic QM developed by Dirac and others in late 1920s. This is a novel interpretation of QM and it is generally based on the Einstein’s idea of relative time, i.e. the lack of simultaneity in different frames of reference. We call it time-relativistic to emphasize that unlike in Special Relativity, we do not deal here with the relativity of motion, but rather we deal with the relativity of time. Although Einstein only considered classical frames of reference moving relative to each other, we suggest extrapolating this notion on the quantum mechanical system and its observer regardless of their relative movement. In our definition, a quantum-mechanical frame of reference is a closed information processing system with a conscious observer. The common thread with special relativity is the realization that clocks will show different time in different frames of reference and an exchange of information, i.e., an act of measurement, is necessary to synchronize the clocks in different frames.
A quantum-mechanical system represents one frame of reference that has its own timeline. An observer is in another frame of reference with its own clock and timeline. Thus, a quantum-mechanical system, which is the object of measurement, and the observer who is the subject that measures it, are in two different reference frames. Before their clocks can be synchronized, an information exchange between the two frames of reference must take place – this is the process of measurement.
Physicists do not like the collapse of the wavefunction because it does not follow from the Schrödinger equation. Mathematicians do not like it because it makes the wavefunction a discontinuous function – something that is very difficult to deal with. Yet we forget that we deal with an almost identical situation every moment of our lives without making a big deal about it. Isn’t it true that the transition between future and past behaves in exactly the same way?
There is an uncanny similarity between the collapse of the wave function and the transition from future into the present. Indeed, future time is characterized by a plurality of amorphous possibilities or, in the language of mathematics, by distribution of probabilities of all possible events, just as a quantum mechanical system is characterized by the wavefunction that describes a distribution of probabilities of all possible states of the system.
Let us consider a flipped coin before it falls down (while the event of heads or tails is still in the future). At this point, the probability of it falling heads up is 50%. In othe words, when the event of a coin falling heads us is still in the future, its probability function is equal 0.5. After the coin is on the ground, the probability of its falling heads up is either 1 or 0 depending on whether or not it landed heads up. In general, any events in the future have a probability between 0 and 1, and any event in the past has a probability of either 1 or 0 depending on whether it happened or not.
The past is distinguished from the future by the fact that all those probabilities have only two possible values: zero or one, i.e. any particular event either has happed or has not happen. The present moment is the point in time when the distribution of probabilities of future events collapse into a single value – zero or one – depending on whether the event in question happened or not. This is exactly the situation we find ourselves in when conducting a quantum-mechanical experiment: from all possible quantum-mechanical states we select only one state that we observe in the experiment – what is referred to as the collapse of the wavefunction. This suggests that what we are dealing with here is the transition between the future into the present.
This transition happens because for as long as there is no exchange of information between the reference frame of a quantum-mechanical system and the reference frame of an observer, the quantum-mechanical system is in the future of the observer. Indeed, until the experiment is conducted, there is no information available about the quantum-mechanical system aside from what we can glean from the Schrödinger equation – a distribution of probabilities. Thus, as far as the observer is concerned, the system is in the future. When the experiment is conducted and the information about the system is obtained, as far as the observer is concerned, the quantum-mechanical system has moved into the observer’s present time.
Let us again reconsider the Schrödinger cat. Before we look inside the box, the cat is in future time with respect to us. Therefore, there is nothing unusual about its entangled state – it’s neither dead nor alive because, as far as we are concerned, the event that will determine the fate of the cat hasn’t happened yet. Once we open the box, which synchronizes the clocks, the cat moves into our present time and, no wonder, we find only one possibility actualized – the cat is either dead or alive. The key to the solution of the Schrödinger cat paradox is to realize that time flows differently in different reference frames associated with a quantum-mechanical system and an observer: what is present in an isolated quantum system is still in the future for an observer until he conducts an experiment which synchronizes the clocks and brings the QM system into the observer’s present – hence the collapse of the wavefunction, hardly a paradox at all. This illustrates how our time-relativistic interpretation demystifies quantum mechanics.
Let us now compare the three possible explanations of what happens with the Schrödinger cat:
| Before box is opened | After box is opened | |
| Classical physics | The atom either decays and kills the cat or doesn’t. At all times, the cat is ether dead or alive | Observer finds the cat either dead or alive. |
| Copenhagen interpretation of QM | The atom exists in an entangled state of decay/non-decay; the cat is in an entangled state of being dead/alive at the same time. | Observer collapses the wavefunction, retroactively “causing” the atom to decay and kill the cat or not. |
| Many-Worlds interpretation of QM | The radioactive atom causes the universe to branch out into two copies: in one, it decays and kills the cat; and in the other, it doesn’t. The cat is alive in one branch of the universe and is dead in the other. | Observer is split into two carbon-copies. One observer finds the cat alive in one universe and the other copy of the observer finds the cat dead in the other universe. |
| Time-relativistic interpretation of QM[††] | Until the measurement, observer’s clock is not synchronized with a clock in the box, each being in separate frames of reference. From the observer’s vantage point, a possible decay of the atom and resulting demise of the cat are indeterminate because they are in the observer’s future. From this point of view, cat is neither dead nor alive simply because it hasn’t had a chance to die yet, as far as the observer is concerned. | Opening of the box, resulting in the exchange of information, synchronizes the clocks in two reference frames, one associated with the observer, and another, associated with the quantum-mechanical system. This brings the quantum-mechanical system into the observer’s present allowing the observer to decide whether the cat is dead or alive. The “collapse of the wavefunction” is nothing more than a transition from future into the present. |
Table 1
Applying our approach to the problem at hand, we can say that before the first observer opened his eyes and looked at the universe, it was, with respect to this observer, in future time. It may be said that it was Adam who synchronized his clock with the universal clock (what Rabbi Hunia ben HaKannah calls the divine years). Therefore, we have two time lines associated with two frames of reference, one connected with the Universe and the other with us, humans.
Conclusion
In this paper we have demonstrated that the apparent contradiction between the “biblical” age of the universe and the cosmological age of the universe can be reconciled based on quantum mechanics in its various interpretations. The common denominator of all of these approaches is that the first human observers, Adam, sets off a new timeline, which coexists with the much older universal timeline originating at the moment of the Big Bang. In the Copenhagen interpretation, Adam collapses the universal wavefunction. In the MWI, Adam realizes only one of many branches of the universal wavefunction based on the antropic principle. In the parallel universes model, Adam causes an interference of the wavefunction distributed between the two parallel universes. In our time-relativistic approach, identifying the collapse of the wavefunction with the transition from future into present, the pre-human history of the universe appears as future until the first observer brings it into his present. Since all of the above approaches are mathematically equivalent to each other, the various interpretations are closely interrelated and, to a large degree, are a matter of taste. They all, however, effectively reconcile the two vastly different ages of the universe.
Interestingly, the Lubavitcher Rebbe, Rabbi Menachem Mendel Schneerson, may have alluded to this approach in one of his talks on the weekly Torah portion “Shoftim.”[19] In this discourse, the Rebbe discusses the Talmudic concept of two types of witnesses: clarifying witnesses and establishing witnesses[20]. The first type of witnesses is called eidei birur, or clarifying witnesses. These witnesses do not consummate the transaction that they witness, but they clarify the transaction if its terms are later disputed. Witnesses to a business transaction are clarifying witnesses. To be sure, a business transaction takes effect regardless of whether witnesses are present. The second type of witnesses is called eidei kiyum, or establishing witnesses. These witnesses are integral part of the transaction that they view, and in their absence, the transaction has no effect. Witnesses to the ceremony of Jewish betrothal (Kidushin) are establishing witnesses, and their testimony establishes the marriage in Jewish law.[21] Without their presence, the marriage does not take effect. Establishing witnesses can also be called upon to clarify the transaction at some later point, but that is not their primary function.
The Rogatchover Gaon[22] explains that the distinction between clarifying witnesses and establishing witnesses is also apparent in the laws of interrogation. As clarifying witnesses perform their primary function when they clarify a matter through testimony in court, they are not technically considered “witnesses” until they testify, and they attain the status of witnesses in beth din (court). The Torah requires beth din to interrogate witnesses before allowing them to attain the status of witnesses. On the other hand, establishing witnesses perform their primary function by simply viewing the transaction, and their status as witnesses is not conferred by beth din. Therefore, beth din does not interrogate establishing witnesses.
The Rebbe draws the parallel with two interpretations in the Zohar,[23] of the verse, “You are my witnesses, says G‑d.”[24] One interpretation is (the simple interpretation of the verse) that it refers to the Jewish people. The second interpretation is that the verse alludes to the sky and earth as witnesses, as another verse states, “I call heaven and earth as witnesses.”[25] According to the Rebbe, the latter interpretation suggests that heaven and earth are clarifying witnesses, whereas the former interpretation, referring to the Jewish People, considers them establishing witnesses, whose testimony establishes the act of creation. The parallel between the Talmudic “establishing witness” and Wheeler’s “participating observer” is remarkable.
Moreover, this discussion sheds light on the question of the interplay between science and faith. Both play important but different roles as respectively clarifying and establishing testimonies to the creation. Recall that in Talmudic law the clarifying witnesses are subjected to interrogation to clarify their fitness as witnessed and the veracity of their testimony. Heaven and earth, which are called “witnesses” by Moses and which, according to the Rebbe, are clarifying witness, need to be thoroughly examined. This is the role of science which seeks to clarify the nature and the laws of the creation by probing and examining heaven and earth, figuratively speaking. Once the clarifying witnesses are examined they can testify. This will happen, according to the Jewish tradition, in the Messianic era when heaven and earth will offer their testimony of the creation and instead of concealing G‑dliness they will bespeak it. The first human observers, Adam and Eve, on the other hand, established the very existence of the world as the establishing witnesses or, in the language of quantum physics, as participating observers, the moment that they ‘witnessed’ its existence.[‡‡] Thus science and faith do not contradict each other but play a complimentary role of respectfully clarifying and establishing witnesses to the creation. As Niels Bohr put it, contraria sunt complimenta.[§§]
[*] Presented at the Fifth Miami International Conference on Torah & Science in Dec. of 2003; to be published in B’Or HaTorah, (2005).
[†] Cosmological models based on the Hubble constant result in 13.7 billion years old Universe. Radioactive dating of elements in old stars suggests a range of 11.5 to 14.1 billion years. Estimates based on the age of the oldest white dwarfs give an age of the Universe of 12.8 billion years. Most recent data finding is based on new results from NASA’s Wilkinson Microwave Anisotropy Probe (WMAP) satellite, launched in 2001, sets the age of the Universe at 14.7 billion years although Cyclic Universe Theory suggests that the Universe may be much older than that.
[‡] According to the Biblical account, Adam and Eve were created simultaneously as one being, only later to be separated into male and female. Therefore, the question of who collapsed the universal wavefunction first – Adam or Eve – does not arise.
[§] Gen. XVIII, 2.
[**] Zohar, Vaerah ???
[††] By time-relativistic interpretation of QM we do not mean the standard special relativistic QM developed by Dirac and others. This is a novel interpretation of QM suggested by the author of the present article, which is generally based on the Einstein’s idea of relative time and the lack of simultaneity in different frames of reference. Although Einstein only considered classical frames of reference moving relative to each other, we suggested extrapolating this notion on the quantum mechanical system and its observer regardless of their relative movement. The common thread is the exchange of information necessary to synchronize the clocks in different frames. See supra.
[‡‡] Jewish people continue this process today by declaring each Friday night on the eve of Shabbat a testimony to the creation of the world (see prayer Vaihulu HaShamaym… in the Liturgy for the Eve of Shabbat). Chasidic philosophy maintains that the world is recreated by G‑d every moment (See Tanya, Shaar Yihud VeHaEmuna). Therefore, just as at the time of Adam and Eve, there is a continuous need for establishing witnesses to reaffirm and establish the act of creation. This role is played today by Jewish people who are the quintessential participating observers in the language of quantum mechanics.
[§§] Contraria sunt complimenta (Lat.) i.e. the opposites are complementary—the device Niels Bohr chose for his coat-of-arms upon receiving knighthood in the Order of Elephant.
[1] Poltorak, Alexander. “On the Age of the Universe.” B’Or HaTorah 13E (Jerusalem: SHAMIR, 2002) pp 19-37.
[2] Rabinowitz, Avi and Branover, Herman. “The Role of the Observer in Halakhah” in Branover H. and Attia I.C (ed.) Science in the Light of Torah (Northvale, NJ: Jason Aronson, 1994). Originally published in Fusion (New York: Feldheim, 1990)
[3] Poltorak, Alexander. Ibid
[4] Midrash Rabbah, Bereishit 1:2; Zohar, 1:134a, vol. II, p. 161b.
[5] Midrash Rabba ???
[6] Kaplan, Aryeh. Immortality, Resurrection and the Age of the Universe: A Kabbalistic View (New York: Ktav Publishing House, 1993).
[7] Sanhedrin 97a.
[8] Avraham ibn Ezra on Leviticus (25:2).
[9] Ramban on Genesis (2:3).
[10] Von Neumann, John. Mathematical Foundations of Quantum Mechanics (Princeton, NJ: Princeton University Press, 1955)
[11] Wigner, Eugene. “Remarks on the Mind-Body Question” in Good, I.J. (ed.) The Scientist speculates: an anthology of partly-baked ideas. (London: Heinemann, 1961).
[12] Weeler, John A. “Genesis and Observership” in Butts R.E. and Hintikka K.J. (ed.) Foundational Problem in the Special Sciences (Dordrecht: Reidel, 1977). Weeler, John A. “Beyond the Black Hole” in Woolf H. (ed.) Some Strangeness in the Proportion: A Centennial Symposium to Celebrate the Achievements of Albert Einstein (Reading, MA: Addison Wesley, 1980).
[13] Rabinowitz, Avi and Branover, Herman. Ibid.
[14] Poltorak, Alexander. Ibid.
[15] H. Everett, Review of Modern Physics, July 1957.
[16] B. S. DeWitt and N. Graham, The Many-Worlds Interpretation of Quantum Mechanics, Princeton Univ. Pr.:1974
[17] Poltorak, Alexander. Ibid.
[18] R’ Nehunya ben HaKanah, Sefer HaTemunah. p.314. See also Kaplan, Aryeh. Immortality, Resurrection, and the Age of the Universe: a Kabbalistic View. (Hoboken, NJ: KTAV, 1993) ch.1, pp.1-16
[19] R’ Schneerson, M.M. Likute Sihot (Brooklyn, NY: Vaad L’Hafotzas Sichos, 1998) v. XIX, Devorim, pp. 188-196.
[20] Kiddushin, 65b.
[21] Ibid.
[22] Responsa Tzafnat Paneach, Dvinsk, Volume 1, 69.
[23] Zohar III, 86
[24] Isaiah 43:10.
[25] Deuteronomy, 30:19


Hello Alexander, very interesting your thesis’s but have you read Gerald shroeder Genesis and big bang, where he proposed base on the comentary of the sages that the time as we know today it’s relative and as najmanides said ” the days of creation where days that contein all generations”
Yes, I am familiar with Dr. Shroeder’s interpretation.
I did not see a reference to Neils Bohr’s experiment re: double slit phenomenon, where an observer collapses the wave function, and in effect stabilizes the world– if you will. I always considered him as the father of quantum physics.
double slit is referenced
Alexander–Quite compelling–I was not familiar with the transition from present to future likened to the “collapse of the wave form” or union of parallel universes and such–is there any literature on this that you would recommend from yourself or others?