By the mouth of two witnesses, or three witnesses, shall the one liable to death be put to death; he shall not be put to death by the mouth of one witness. (Devarim-Deuteronomy 17:6)
I wrote about witnesses in my earlier post imaginatively called Witnesses. As Deuteronomy, restates many mitzvoth (commandments) introduced earlier, which is why it is also called Mishneh Torah – the repetition of Torah – the portion Shoftim-Judges restates the law of witnesses first introduced in in the book of Bamidbar-Numbers, portion Massei. So we shall revisit this fascinating subject.

The Judgment of the Sanhedrin: “He is Guilty!” (1892 painting by Nikolai Ge)
I. An accused criminal and a Schrödinger cat
Most criminals are convicted in the US bases on circumstantial evidence. Rare is the case when a jury gets to hear an eyewitness. For example, most of the evidence against Timothy McVeigh was circumstantial. A law professor at the University of Michigan, Robert Precht, said commenting on McVeigh’s trial, “Circumstantial evidence can be, and often is much more powerful than direct evidence.” Logically, this makes a lot of sense. Indeed, people lie intentionally or make innocent mistakes. A “smoking gun,” fingerprints, DNA evidence are examples of objective circumstantial evidence that often have greater weight in the minds of jurors deliberating the guilt of an accused criminal than a testimony of an eye witness whose credibility can be easily impeached. Consequently, many prosecutors prefer to rely on circumstantial evidence. No so in Jewish law. As the Torah teaches us in this Torah portion, only by the testimony of eyewitnesses can a Jewish court convict an accused criminal. This is not easy to understand. Doesn’t this mean that most criminals go free? Perhaps so… but the logic of the Torah can be easily understood from the point of view of Quantum Mechanics (QM).
In QM a particle or an ensemble of particles is described by a wavefunction obeying the Schrödinger equation. The wavefunction (or, more precisely, square amplitude of the wavefunction) describes the probability of finding a particle in the given area of the phase space. In other words, the wavefunction does not predict exact values for physical characteristics of the particle – only a probability distribution of finding some values more likely than others. However, when we measure a quantum-mechanical system, say a position of a subatomic particle, we always get a precise value for the characteristic we measure. It is if the distribution of probabilities or the probability “cloud” suddenly collapses into a single value. In QM, this is referred to as the collapse of the wavefunction. The trouble is, this collapse of the wavefunction does follow from the Schrödinger equation of from any other principle of the QM. It is not at all predicted by the QM and added ad hoc to explain experimental findings. When we study the equations, we see one picture. When we measure the system, we get another picture. This paradox is also known as the Measurement Problem.
The Measurement Problem leads to such strange phenomena as a Schrödinger cat. The cat is described by a wavefunction, which is a linear superposition of two states: the cat is alive, and the cat is dead. So the poor feline is in a surreal state of suspended animation, stuck somewhere between being dead or alive. It takes an observer to collapse the wavefunction of the cat to bring it to a certainty: either being dead or alive.
Some of the greatest minds of the 20th century, including Jewish-Hungarian genius mathematician, John Von Neumann, Nobel laureate in physics, Eugene Wigner, and Princeton physics professor, late John Archibald Wheeler (Richard Feynman was his student), all thought that only human consciousness can collapse the wavefunction. This lead John Wheeler to coin the term, participatory observer, which means that an act of observation is not passive – the observer participates in creating reality by collapsing the wavefunction.
From the point of view of structural analysis, the Torah approach is parallel to the quantum-mechanical approach: a suspect, which may be innocent or guilty, like the Schrödinger cat, is in a state of linear superposition of two states: guilty and innocent. Only an eyewitness, i.e., a conscious observer, can collapse his wavefunction and bring certainty in place of uncertainty. This is why, in my humble opinion, the Torah requires an eyewitness’s testimony to convict a suspect — we need an eyewitness, a participating observer, to collapse the “wavefunction” of the accuse and resolve the uncertainty.
II Why One Eyewitness Is Not Enough?
You may have seen movies with the Perry Mason moment, when the witness on the witness stand points to the suspect sitting in the courtroom exclaiming, “He did it!” This makes it easy for the jury to reach a verdict beyond a reasonable doubt.
In QM, it takes only one observer to collapse the wavefunction. If so, following our logic, one eyewitness should be enough to convict a criminal. Why than Torah requires more than one witness? Why one eyewitness, no matter how respected (in the words of the Talmud, even if this witness is Moses himself), is not enough?
The obvious explanation is that one witness cannot be properly interrogated, his testimony cannot be compared with the testimony of another eyewitness. The Torah takes the principle of “innocent until found guilty” to a whole new level. Torah purposely makes convicting the accused very difficult, even almost impossible. All of the horrible punishments enumerated by the Torah, such as stoning, decapitation, strangulation – are meant as a deterrent – “And people will hear and they will be afraid and thus you will eradicate this evil from Israel,” is a common refrain in the Torah. Therefore, the Torah requires at least two witnesses so that judges can interrogate them pitting the testimony of one against the other so that inconsistency can be found and the testimony would be thrown out of court. We need not worry that many a criminal would go free. Ultimately, those who committed heinous crimes will not go unpunished, but the punishment will come from the “hands of Heaven.” This teaches us not to be arrogant and not to Play G‑d, but rather rely on Him to carry out justice in the world.
Philo praised the requirement that a court should not rely on the testimony of a single witness as an “excellent commandment.” Philo was concerned that an individual may be deceived by a false first impression. Moreover, why should a court take the word of one witness against the word of the accused? Where there is no preponderance of the evidence, the judgment should not be made, argued Philo.
Perhaps another reason can be a profound realization that human knowledge is imperfect and is subject to uncertainty. Only G‑d, who is omniscient, has perfect knowledge because He knows all by knowing Himself. It is a statement of humility, to acknowledge that one man can never have the perfect knowledge and certainty, which are domains of G‑d. This may be another reason, perhaps, that Torah requires more than one witness to convict a suspect of a crime. Even then, we realize that testimony of two or more witnesses, at best, is an approximation of the perfect knowledge of G‑d. This is our way of dealing with the inherent uncertainty of human knowledge. In the words of Karl Popper, a prominent 20th-century philosopher of science, we can only be certain that a theory is wrong; we can never be sure that it is right. Torah taught us this long before Popper.
Uncertainty, interrogating two witnesses… These concepts invoke airy similarity with the Heisenberg Uncertainty Principle. According to the Uncertainty Principle, which is the basis of Quantum physics, we can never be certain of the values of two complementary properties, we can never measure such properties with an unlimited degree of precision. Take for example such pairs of complementary properties as position and momentum, or time and energy. According to the Uncertainty Principle, the products of uncertainties in measurements of these properties must always be equal or greater than the Plank constant. If, for example, ∆x is the uncertainty in the measurement of the position of a particle and ∆p is the uncertainty in the measurement of the momentum of this particle, then
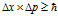
Similarly, if ∆t is the uncertainty in the measurement of time and ∆E is the uncertainty in the measurement of energy, than
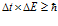
Let us now consider the testimony of two witnesses. It is easy to understand that they are complimentary in a quantum-mechanical sense – the more precise is one testimony, the more imprecise must be the other in order not to contradict the first. Say, for example, the first witness testifies that the crime took place in the morning. Although the second witness is not aware of the testimony of the first witness – they are interrogated separately – it is easy for him to also say that the crime was committed in the morning. However, if the first witness says the crime was committed at 10:01 AM and the second witness says it was committed at 10:02, the two testimonies are inconsistent and are thrown out of court. So, not to contradict the first witness, the second witness should say that the crime was committed sometime in the morning but he doesn’t remember the exact hour. The more precise is the testimony of the first witness, the vaguer should be the testimony of the second witness not to contradict the first. Just as in Quantum Mechanics, were the product of uncertainties in measurements of complementary properties cannot be zero, here too, the product of uncertainties in testimonies of two witnesses cannot be zero. This is used by judges to find inconsistencies in testimonies of the witnesses to disqualify them and to acquit the accused. Since this is the goal, the Torah prescribes an easy mechanism to accomplish it, in the meanwhile, teaching us something about Quantum Physics.
III Two or Three Witnesses
According to the Torah, a suspect cannot be convicted by the testimony of one witness. “By the mouth of two witnesses, or three witnesses…” Why does the Torah say, “two witnesses, or three witnesses”? If two witnesses are enough, surely three would also be enough!
The Talmud (Makos, 5b) explains that if the third witness contradicts two other witnesses, the testimony is inadmissible. Although, in deciding halachic matters (questions of religious observance) the court goes according to the majority, in criminal matters, surprisingly, this is not the case. Even if in a group of 100 witnesses, 99 of them corroborate each other’s testimony, but one witness contradicts them, all 100 witnesses are disqualified and their testimony is thrown out of court. All witnesses are treated as a single group. This is hard to understand as it appears counter-intuitive.
The Talmud further explains that all witnesses offering their testimony about a crime must have observed not only the crime but must give the testimony about each other during that crime. At the first blush, this makes little sense – what difference does it make whether or not witnesses saw each other during the crime? So long as they all saw the crime and give identical testimony this should have been enough!
It turns out, this detail about the law of witnesses is the key to understanding why all witnesses are treated as a single group. By seeing each other, witnesses get entangled with each other. In the language of quantum mechanics, they share the same state, i.e., they are described by the same wavefunction. When mountain-climbers scale a summit being tight to each other by a single rope, if one falls, he or she can pull down the whole group with them. Here too, because all witnesses are entangled, one witness can invalidate the entire group no matter how large. Witnesses in Jewish law must not only see the crime but see and be seen by each other. This gives a new meaning to the old expression – see and be seen.

The Sanhedrin (illustration from the 1883 People’s Cyclopedia of Universal Knowledge)

Your last point is the most interesting–because this is counter-intuitive. I think we could say categorically that no classic logician would come to such a conclusion.
So, although Torah is not speaking openly about QM (and neither is it providing a real instance of a measurable “spooky action at a distance”), nevertheless it is providing us the keys—a unique form of logic that unlocks the secrets of the universe.