And he [Avraham] spoke with them, saying, “…Listen to me and entreat for me to Ephron the son of Zohar. That he may give me the Machpelah (Double) Cave, which belongs to him, which is at the end of his field…” (Genesis 23:8-9)
double: A house with an upper story over it. Another interpretation: because it was doubled with couples (Er. 53a) (Rashi on Genesis 23:9)
In the Torah portion Chayei Sarah, Avraham purchases a Double Cave, Machpelah, as the ancestral burial plot. Almost all classical Biblical commentators interpret Machpelah (that is, “double”) to mean a cave with two chambers. Rashi takes an entirely different approach and states that the cave was known for a two-story house built on top of it. So, the word Machpelah refers not to the cave itself, but to the house built on top of the cave. Even stranger is that Rashi offers an alternative interpretation saying the word “double” may also refer to the couples of patriarchs that are buried there—Adam and Eve, Abraham and Sarah, Isaac and Rebeca, and Jacob and Leah. What is the connection between these two very different interpretations?
There is a deep mystery in physics. Although it is right at the surface steering in our eyes, you won’t find any mention of it in any physics textbook; you won’t hear any professor mentioning it in a lecture (I did, but I never heard of anyone else speaking of it). You don’t even have to have a Ph.D. in physics to understand it – any high school student studying Newtonian mechanics should be able to grasp it. Here it is.
The Second Law of Newton states that for any body,
a × m = F, or a = 1/m × F,
where a is the acceleration of the body, m is the mass of the body, and F is the total force acting on the body. Essentially, the second law of Newton states that the acceleration a of a body with the mass m is proportional to the force F acting on the body (here, the bold letters denote vectors, that is quantities which have both a magnitude and a direction; velocity, acceleration, and force are vectors, whereas mass is a scalar—a quantity without a direction).
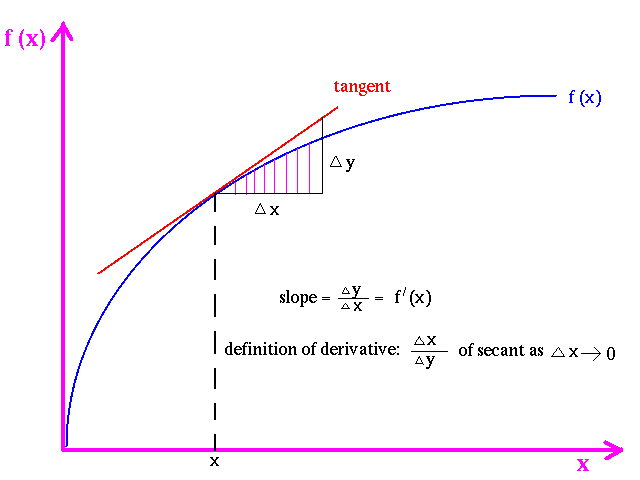
Where is the mystery, you may ask? For that, we need a bit of math. The velocity of an object is the first derivative of the objects’ position in space over time: v = dx/dt.
Simply speaking, a derivative measures the sensitivity to change of the function value (output value) with respect to a change in its argument (input value). The derivative of a function is the slope of the tangent line to the graph of the function at that point.
A house built on top of the surface of the earth is tangent to the surface as well:

The acceleration is a velocity of the velocity, i.e., a derivative of the velocity over time: a = dv/dt.
That makes it the second derivative (a derivative of the derivative) of the position over time: a = d2x/dt2.
The derivative of a function is the speed with which this function changes with the change of the argument. The derivative itself is a function—a mathematical structure we build on top of the original function. Because it is a function in its own right, we can take a derivative of that function—the second derivative of the original function and build yet another structure “on top” of the original function, the “upper story” over it. Thus, metaphorically speaking, the second derivative can be thought of as a two-story structure erected on top of the original function.
The second derivative pops up everywhere in physics and seems to represent a fundamental law of dynamics.

Eugene Wigner
During his Nobel acceptance speech, the physicist Eugene Wigner said that the role of science is to separate patterns from noise. This was one of the most insightful statements I heard about the nature of science. This is what Newton did with his Second Law.
Let us imagine that we live before Newton, and we are trying to study the motion of an object. We would observe such motion numerous times, noting the correspondence between the position of the object and the time at which this position is measured. At the end of a long experiment, we would accumulate a large amount of data—points on the graph plotting the position of the object with the course of time. We might imagine that some of this data is random (that is, noise), and some represent some pattern—the yet unknown law of physics. All dynamical processes in physics are described by differential equations (such as the Second Law of Newton). If we were to assume that our unknown pattern is described by a differential equation of the first-order (the first derivative), to solve it, we’d have to integrate, as the integral is the opposite of the derivative. However, the derivative of a constant is always zero, which means that when we reverse the operation of the differentiation by taking an integral, we can only know the answer up to a constant. What this means is that if our pattern is described by a differential equation of the first order (the first derivative), we will have a layer of random noise represented by the constants popping up during the integration. To get rid of them, we need to select the initial conditions. In the case of a moving object, we’d need to know the initial position of the object.
If, however, our pattern is described by the differential equation of the second-order (the second derivative), to solve it, we’d need to integrate twice, producing two sets of constants and, therefore, two layers of random noise. To get rid of this noise, we’d need to know two sets of initial conditions. In the case of a moving object, we’d need to know its initial position and initial velocity.
The genius of Newton was to guess that the fundamental law of mechanics (and, as it turned out later, of dynamics in general) is the differential equation of the second-order (the second derivative). This is why in mechanics, to predict a future position of an object at some point in time, we need to know its initial position and velocity—we need a couple of initial conditions. In mathematics, the initial conditions are progenitors of the future value of the function—“patriarchs,” if it were.
Now, all pieces of the puzzle fit together: the structure with the second story on top of the cave in the first Rashi’s interpretation is a metaphor of the second derivative—the second story structure we build on top of the original function. The couples buried in the cave refer to a couple of initial conditions necessary to solve the equation with the second derivative.
While the second derivatives are ubiquitous in physics, I always thought that this is a universal principle. For some reason, whenever we want to study the evolution of a dynamical system in time, it will turn out to be the second derivative that represents the pattern with two layers of random noise associated with it.
This is why trying to curve-fit the past market behavior to predict future stock prices is the fool’s errand—you’d be mixing together patterns with noise. You may be able to predict the future stock price (or the price of any commodity or financial instrument) by considering the second derivative of the price over time. If you want to get rich, I just told you how.
Even in medicine, when we take tests, it’s not so much the current value of the test that matters, but how it “accelerates” in time, that is, the second derivative. Indeed, in one study of the relevance of PSA as the predictive marker for prostate cancer, the study showed that it was the second derivative—the acceleration in the rise of PSA—that had the greatest predictive value. Indeed, the second derivative rules! This is not to say that static tests that show a snapshot in time are not useful. But if we can repeat a test often and calculate the second derivative, that would give us much greater diagnostic value.
Perhaps, Rashi was hitting to us at this secret by explaining the meaning of the word Machpelah as the two-story structure on top of the cave.


Leave A Comment