Maarat HaMachpelah – Double Cave

Give me the Machpelah (double) Cave

Genesis 23:9

The first legal acquisition of land in Israel takes place in this Torah portion, Chayei Sarah, when Abraham purchases a double cave, Maarat HaMachpelah, in the city of Chevron (Hebron) as an ancestral burial plot. Today, the immense rectangular structure built over the cave more than 2000 years ago during Herodian era is the oldest house of worship in the world in continuous use.

Biblical commentator Rashi explains that the cave was called Machpelah (lit., double) because it had two structures—an upper chamber and a lower chamber. (Another explanation given in the Talmud relates the name of this cave to thee couples buried there—Abraham and Sarah, Isaac and Rebecca, and Jacob and Leah. According to Kabbalah, Adam and Eve are buried there as well (Zohar, Ruth 96).

Cave of the Patriarchs

A Midrash explains that the reason this cave had two chambers—the upper and the lower—is because it reflects the structure of Gan Eiden (Paradise — the Garden of Eden), which also has two levels—Gan Eiden HaElion (the Higher Paradise) and Gan Eiden HaTachton (the lower Paradise).

The Cave of the Patriarchs is not the only “double” structure in the Torah. When Jacob returns to the land of Canaan after sojourning with Laban, he encounters the angels:

When he saw them, Jacob said, “this is a camp of G‑d,” and he named the place Machanaim. (Gen. 32.2)

Rashi interprets the word Machanayin as a “double-camp”—double, because Jacob was escorted by one group of angels of the diaspora and met by another group of angels of the Land of Israel—the latter higher than the former.

This Midrash points to an important principle of Jewish mysticism—the structure of the spiritual worlds is reflected in the physical world. The physical cave had the same structure as the spiritual paradise—the world of souls.

The Cave of Machpelah, 1877 – Vincent van Gogh

Where in physics do we have an example of this doubling up? The phase space, of course! Newtonian classical mechanics operates in a familiar three-dimensional space. However, the second law of Newton is a differential equation of the second order (acceleration is the second derivative of coordinates over time). To solve this equation we need two sets of initial conditions—three initial coordinates (X₀, Y₀, Z₀) of a body and its three components of the initial velocity (V_x, V_y, V_z). Therefore it is more convenient to describe the motion of the body in a six-dimensional phase space that has three spatial coordinates (X, Y, Z) and three momenta coordinates (P_x, P_y, P_z) (momentum is a product of velocity and mass). The concept of the phase space that represents all possible states of the system was first developed at the end of the nineteenth century by

Ludwig Boltzmann

Ludwig Boltzmann and Henry Poincaré. This six-dimensional phase space is, in a sense, “double” space comprised of a regular three-dimensional space and an additional three-dimensional space of momenta.

Henry Poincaré

The analogy goes even further. Just as in Paradise, two levels are not on the same level, but one, Higher Paradise, is above the other, Lower Paradise, and just as in Maarat HaMachpelah, two chambers are one above the other, so is in the phase space six dimensions are split into two levels 3+3 one “above” the other. The three dimensions of momenta can be viewed to be “above” the three spatial dimensions, as it were, because momentum (which is a product of mass and velocity) is a derivative of the spatial coordinates over time, i.e., it’s a three-dimensional structure built over the basic three-dimensional space.

In quantum mechanics the phase space plays a much more important role than in classical mechanics, because of the Heisenberg uncertainty principle that connects coordinates with momenta:

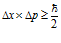
Werner Heisenberg

Where ∆x is the uncertainty in the measurement of coordinates of a particle, ∆p is the uncertainty in the measurement of the momentum of the particle, and ћ is the Plank constant. This inequality ties together spatial coordinates and momenta, which in Quantum Mechanics become “complementary” observables.

The convenience of using phase space stems from the fact that each point represents a complete state of a physics system. And to describe the complete state of a physical system it is necessary to double up space from three dimensions to six dimensions.

Thus we see that the spiritual concept of double space in the Paradise reflected in double cave of Maarat HaMachpelah is further reflected in a “double” phase space used in classical and quantum mechanics.

The Midrash states that Cave of Machpelah (a.k.a. Cave of the Patriarchs) is the gateway to Gan Eden (Paradise). Jewish mystical tradition Kabbalah teaches that Maarat HaMachpelah is the gate through which souls enter Gan Eden. A connection to the uncertainty principle is not coincidental. As Rabbi Aryeh Kaplan explained his book “Inner Space: Introduction to Kabbalah, Meditation and Prophecy,” the main difference between physical and spiritual is space–the physical world is defined by space, whereas in the spiritual word the space, as we know it, does not exist (although, there is a conceptual space in spiritual world where proximity is defined by conceptual similarity of ideas). Therefore, the more physical space is eroded (by losing its concreteness and well-defined properties), the closer we get to spiritual domain.  It is the quantum uncertainty in the physical world that blurs the boundary between physical and spiritual and allows the physical realm to “touch,” as it were, the spiritual realm.  Perhaps this is why Maarat HaMachpelah is a portal into the Paradise—the world of the souls.

This uncertainty extends to the Patriarchs and Matriarchs buried in the Cave of Machpelah. They are neither dead nor alive but they are in a state of superposition—in the words of the Midrash, the Patriarch “slumber” in the Cave.  From time to time, they rise and beg for mercy for their children. May the merit of our Patriarchs and Matriarchs protect us!

Maarat HaMachpelah by Alex Levin.