Congratulations to Roger Penrose, Reinhard Genzel, and Andrea Ghez for wining the 2020 Nobel Prize in Physics for their contributions to establishing the existence of black holes.

A black hole is an object with an infinite density of matter and curvature of space-time. Black holes typically form when a massive star (at least ten times the mass of the sun) runs out of fuel, and the outward pressure of nuclear explosions inside the star can no longer compensate for the inward pressure of gravity. When that happens, the star collapses in a phenomenal explosion called a supernova. All the matter of the star implodes into the singularity—the center of the star. According to Einstein’s general theory of relativity, the density and space-time curvature at the center become infinite. In the real world, of course, no infinities exist. This suggests that the general theory of relativity is incomplete. It is likely to be replaced by a quantum theory of gravity, which will better explain black holes’ physics avoiding infinities. A black hole’s unique feature is the event horizon—a sphere of no-return from which no mass or even light can escape. The latter makes any black hole invisible. If we were to send a spaceship towards a black hole and continue to watch the craft through a telescope, it would appear to us to slow down as it approached the black hole, finally freezing at the event horizon. The spaceship would have, of course, fallen through the event horizon and sucked into the center of the black hole, but all we’d see is the image of the spaceship forever frozen at the event horizon. This is because, according to the general theory of relativity, the gravitational field slows down time. As the spacecraft is approaching the black hole, from our vantage point, time slows down until it “stops” at the event horizon (in the frame of reference of the space sheep, time flows as before while it crosses the event horizon).

While predicted by the Schwarzschild solution of Einstein’s equations, until Penrose, they remained hypothetical objects. In his 1965 paper, British mathematical physicist Sir Roger Penrose showed that black holes are not a figment of theorists’ imagination, but they can and predictably do form in nature. Penrose, who is of Russian-Jewish ancestry (his grandmother was a concerting pianist Sonia Natanson who left Russia at the end of the 19th century), introduced the concept of a “trapped surface.” This closed two-dimensional surface deflects light rays toward the center of the black hole. In special and general relativity, time and space are unified into a four-dimensional space-time continuum. Penrose showed that inside the trapped surface, time and space switch roles—it is time that shows the direction towards the center of the black hole. Consequently, escaping from the black hole is as likely as traveling backward in time.

Astronomers have been looking for any signs of black holes for a long time. In 1931,  Karl Jansky detected a radio signal coming from the direction of the constellation Sagittarius. In 1974, astronomers Bruce Balick and Robert Brown found a bright and compact object in the galactic center, Sagittarius A*. In the early 2000s, German astronomer Reinhard Genzel and his American rival, Andrea Ghez with their teams, have been tracking nearby stars’ motions.

Both teams independently identified a star called S2, whose orbit passed close to Sagittarius A* and whose trajectory indicated that Sagittarius A* could only be a supermassive black hole.

Classical (non-relativistic) black holes were first theorized already in the eighteen century. In 1783, in his talk before the Royal Society, Englishman John Michell speculated that the light would not escape gravity’s force on a sufficiently large planet. He concluded, “Should such an object really exist in nature, its light could never reach us.” In 1796,  the French mathematician, physicist, and astronomer Pierre-Simon de Laplace published a book Exposition du Système du Monde. In this book, Laplace, who followed Newton’s corpuscular theory of light, speculated about massive stars from which no light could escape. He called such star corps obscur, that is, a “dark body.” These speculations were forgotten until young German-Jewish physicist Karl Schwarzschild published his exact solution of Einstein’s field equations for a spherical star that predicted black holes.

My own interest in black holes started in 1970 when I was 13 years old. I didn’t know the general theory of relativity yet, but I already studied the special theory of relativity by that time. I decided to use simple mathematics of special relativity to construct a toy model of black holes. By postulating the maximum density of matter as the second invariant of the theory (in addition to the maximum speed of light), I managed to calculate the radius of a black hole, which remarkable coincided (within a factor of 2) with Schwarzschild radius—the result of the Schwarzschild solution of the equations of general relativity. I never published this result as I considered it a child’s play. Only much later, I realized that I was onto something—what I effectively constructed was a version of the so-called doubly-special theory of relativity. At least I can sleep soundly at night, with no worries of being woken up by an early-morning phone call from Sweden.

As my current interests lie in the intersection of physics and Judaism and, particularly, in finding structural parallels between the two, I suggest that the physical concept of a black hole is hinted at in the Kabbalistic doctrine of Tzimtzum as described in the books of Bahir, Zohar, and Etz Chaim. The most explicit description of the Tzimtzum is given by Rabbi Chayim Vital in the name of his teacher, the Ari-zal, in Etz Chaim:

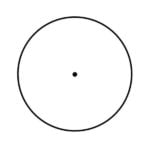
…The Infinite [Light] ([Ohr] Ein Sof) contracted Himself at its mid-point in the exact center of its light…:

The contraction was completely uniform around the mid-point, so that the void was uniformly circular on all sides…

The_Primordial_Space

Here is a clear description of the contraction of the light into a point of singularity—a characteristic property of the black hole. Furthermore, the circle drawn by Chayim Vital appears to me as a hint to the event horizon. If that wasn’t enough, Zohar uses a metaphor of the Lamp of Darkness (Botzina de Kardenuta) for Tzimtzum. Bahir similarly quotes the verse from Job: “And now they do not see light, it is brilliant in the skies…” (Job 37:21), using darkness as a metaphor for Tzimtzum. Were Bahir and Zohar hinting at Pascale’s corps obscure (dark body) now called black hole?