To Mendel
Almost three years ago, in December of 2019, I posted an essay, “The Tree of Knowledge as a Metaphor for Superposition of States and Heisenberg’s Uncertainty Principle.” The manuscript of that essay contained an addendum with a short primer on the superposition of states in quantum mechanics and quantum-mechanical treatment of the primordial sin. It expressed the ideas of Maimonides about primordial sin in precise mathematical formulas proving the exact parallel between the fruit of the tree of knowledge of good and evil and a quantum eraser. Realizing that only people familiar with the formalism of quantum mechanics would understand that part of the essay and fearing losing my readers, I decided to omit the addendum entirely. However, the addendum is arguably the most interesting part of the essay, because it provides a rare example of a rigorous mathematical treatment of a theological concept based on the biblical narrative. I finally decided to publish my old essay (slightly edited) with the mathematical addendum in honor of the 17th birthday of our dear grandson, Medel. I wish him great success in studying Torah and quantum mechanics.
***
And out of the ground made the Lord God to grow every tree that is pleasant to the sight, and good for food; and the tree of life also in the midst of the garden, and the tree of the knowledge of good and evil.
Genesis 2:9
And the Lord God commanded the man, saying: “Of every tree of the garden thou mayest freely eat; but of the tree of the knowledge of good and evil, thou shalt not eat of it; for in the day that thou eatest thereof thou shalt surely die.”
Genesis 2:16–17
Primordial Sin
Upon creating Adam and Eve, G‑d permitted them to eat any fruit from the Garden of Eden, except for the forbidden fruit—the fruit of the Tree of Knowledge. Disregarding this injunction, Adam and Eve (in Hebrew, Ḥavah) ate the forbidden fruit and forever changed the history of the world. This may be one of the most bizarre stories in the Torah. There are different opinions about what was the forbidden fruit—grapes, a fig, an olive… Most of us regularly eat grapes, figs, and olives. However, we become no smarter or less moral from eating these fruits. How are we to understand this?
Many questions beg to be answered. What is the significance of the tree being called the Tree of Knowledge (in Hebrew, Eitz HaDa’at)? What knowledge did Adam and Eve acquire by eating its fruit? Why was the fruit of the Tree of Knowledge forbidden? Moreover, why was this sin so catastrophic that it merited punishment with death and the loss of Paradise?
Before the commission of this sin, the first humans had freedom of choice—they knew true and false, right and wrong; they knew that eating the forbidden food of the Tree of Knowledge was wrong, because they had been told so by G‑d Himself. In fact, the only thing they knew was true (in Hebrew, emet) and false (in Hebrew, sheker). The concepts of good (in Hebrew, tov) and bad (in Hebrew, rah) were unknown to Adam and Eve before the Sin of the Tree of Knowledge (Ḥet Eitz HaDa’at). It was precisely this knowledge that they acquired by eating the forbidden fruit. Presumably, the Tree of Knowledge was more fully called the “tree of the knowledge of good and evil” for no other reason than that it was the source of the knowledge of good (tov) and bad (or evil—rah). Indeed, in attempting to persuade Eve to eat the forbidden fruit, the cunning serpent suggests that as the very reason that G‑d did not want them to eat from the tree of the knowledge of good and evil:
“For G‑d doth know that in the day ye eat thereof, then your eyes shall be opened, and ye shall be as G‑d, knowing good and evil.”
Genesis 3:5
By eating from the Tree of Knowledge, Adam and Eve acquired the knowledge of good (tov) and bad (rah). What was so terrible about them acquiring this knowledge that they deserved capital punishment? What is wrong with knowing good and bad, and how does it differ from knowing true and false or right and wrong?
Maimonides
In his Guide for the Perplexed (Moreh Nevukhim), Maimonides[1] explains that the better Adam (and Eve) understood the concepts of good and bad, the less they were able to differentiate true and false or judge right from wrong:
…the intellect, which was granted to man as the highest endowment, was bestowed on him before his disobedience. With reference to this gift, the Torah states that “man was created in the form and likeness of God.” . . . Through the intellect man distinguishes between the true and the false. This faculty Adam possessed perfectly and completely. . . . Thus, it is the function of the intellect to discriminate between the true and the false—a distinction which is applicable to all objects of intellectual perception. . . . When Adam was yet in a state of innocence, and was guided solely by reflection and reason . . . he was not at all able to follow or to understand the principles of apparent truths [i.e., moral issues of good and bad]; the most manifest impropriety, viz., to appear in a state of nudity, was nothing unbecoming according to his idea: he could not comprehend why it should be so. After man’s disobedience, however, when he began to give way to desires which had their source in his imagination and to the gratification of his bodily appetites, as it is said, “And the wife saw that the tree was good for food and delightful to the eyes” (Gen. 3:6), he was punished by the loss of part of that intellectual faculty which he had previously possessed. . . . Then he fully understood the magnitude of the loss he had sustained, what he had forfeited. . . . Reflecting on his condition, the Psalmist says, “Adam, unable to dwell in dignity, was brought to the level of the dumb beast” (Ps. 49:13).
The Guide for the Perplexed, Part 1, Ch. 2
This is very perplexing, indeed! Maimonides is telling us that so long as Adam (and Eve, of course) had been granted intellectual faculties, which provided the ability to know true and false and discern right from wrong, Adam and Eve were unable to comprehend the notions of good and bad. To wit, they did not see anything wrong in being naked. However, after the sin, the situation reversed—having gained the ability to see good and bad (and, consequently, becoming ashamed of their nakedness), the first humans lost some of their intellectual prowess and the ability to know true and false. How are we to understand this? Why does the knowledge of good and bad preclude—or why is it incompatible with—the knowledge of right and wrong?
The Heisenberg Uncertainty Principle
Let us summarize what Maimonides says: Adam could know either true and false (right and wrong), or good and bad, but not both. The more he learned the latter, the less he knew the former. This is structurally similar to the Heisenberg uncertainty principle in quantum mechanics.[2]
The essence of the uncertainty principle, first formulated by Werner Heisenberg in 1927, is that two complementary variables[3] cannot be known simultaneously with precision—the more precisely we measure one variable, the more uncertain the other variable becomes. For example, the more precisely we know the position of a particle, the less certain we are of its momentum, and vice versa.[4] In quantum mechanics, it is always a trade-off: the more we know of one characteristic of an object, the less we know of the other complementary characteristic.
In the story of the Tree of Knowledge, we are presented with a pair of complementary characteristics: truth and false (right and wrong) on the one hand, and good and bad (evil) on the other. This is why the tree is called the tree of the knowledge of good and evil—because by tasting its fruit the first humans acquired knowledge of good and evil, but lost their knowledge of right and wrong.
The Superposition of States
We touched on quantum superposition earlier in many posts, including “Two Beginnings.” Let us now examine more closely the superposition of states in quantum mechanics.
In his book, Quantum Mechanics and Experience,[5] David Albert gives the following example, as paraphrased here.
Let us suppose that a subatomic particle (say, an electron) has a property we are going to call “color” (it could be the spin of an electron, or the polarization of a photon, etc.). Whatever we mean by “color,” this is a binary property that has only two values—black and white. We can build a color box that has three apertures: one for letting in all (that is, both types of) electrons, one for letting out black electrons, and one for letting out white electrons. The color box does not change the color of the particles that enter it. If we were to send into it a single white electron, it would always (100% of the time) exit through the white aperture and, likewise, if we were to send in a single black electron, it would always exit through the black aperture. The only thing the color box does is to test the color of the electrons and to sort them accordingly. It is a color-sorting apparatus, nothing more.
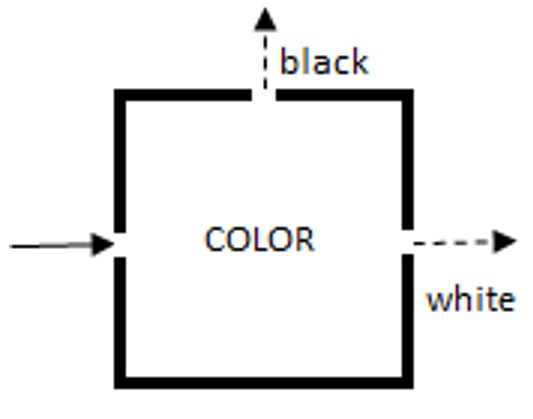
If we mix some black electrons with some white electrons and send them all through the inlet aperture on the left of the box as shown in Figure 1, all the black electrons will exit through the black aperture at the top of the box, and all the white electrons will exit through the white aperture on the right.
Let us suppose that a particle (say, an electron) also has a property we are going to call “hardness.” Like color, hardness is a binary property that has only two values—in this case, hard and soft. We can also build a hardness box that has three apertures: one for letting electrons in, one for letting out hard electrons, and one for letting out soft electrons.

If we mix some hard electrons and soft electrons together and send them through the inlet aperture on the left, all the hard electrons will exit through the hard aperture on the top of the box, and all the soft electrons will exit through the soft aperture on the right, as shown in Figure 2. We build the hardness box so that it does not change the hardness of the particles that enter it. If we were to send a single soft electron into the inlet aperture, it would always (100% of the time) exit through the soft aperture. Similarly, if we were to send in a single hard electron, it would always exit through the hard aperture. The only thing the hardness box does is to test for hardness and sort the electrons accordingly. It is a hardness sorting apparatus, nothing more.
Let us now line up three boxes: a color box, a hardness box, and another color box.
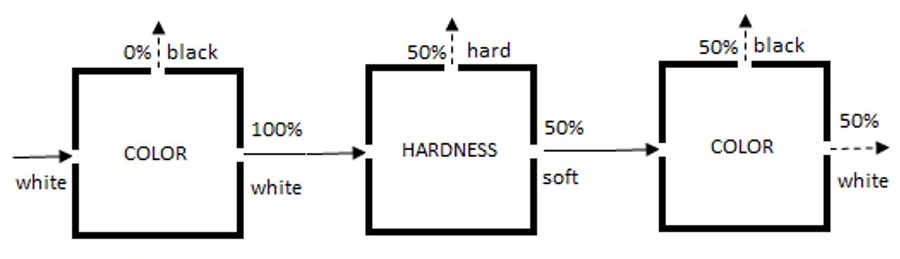
In this experiment, we send only white electrons into the first color box shown on the left of Figure 3. We already know that the color box does not change the color of the particles that pass through it. Therefore, we expect to see 100% of the electrons exiting through the white aperture on the right of the color box. And this is exactly what happens. The white electrons exiting the first color box now enter the hardness box in the middle of Figure 3. The hardness box sorts out the electrons according to their hardness characteristic, with 50% of the electrons exiting through the hard aperture (those are the hard electrons) and 50% exiting through the soft aperture (those are the soft electrons). Now, let us feed all soft electrons exiting from the soft aperture into the second color box on the right of Figure 3. What do we expect to see? We should reasonably expect to see all those electrons exiting the second color box through the white aperture. Indeed, since we sent only white electrons into the middle box, and the middle box supposedly does nothing to these electrons except for checking their hardness, their color should not—or so it seems—be affected. But surprisingly, this is not what happens. In the second color box, fifty percent of the electrons exit through the white aperture, and 50% of the electrons exit through the black aperture. This means that the second color box encountered 50% white electrons and 50% black electrons. But from where did the black electrons come?
This paradoxical result has been verified in countless experiments, which invariably produce the same outcome. It turns out that as soon as we discover information about the hardness of the electrons, we erase all knowledge about their color characteristics. Although we started knowing that 100% of the electrons entering the first color box were white, after measuring electron hardness in the hardness box, this information is lost, which means that there is an equal probability of finding at random a white or a black electron at the end of the three-box process. It is not that the electrons are “actually” white, but the hardness box changes the color of some of the electrons—this is not the case. The hardness box does not change the color, but in the process of measuring the hardness of the electrons the hardness box erases any information about their color, which means we have an equal probability of finding a white color or a black one. (Recall that quantum mechanics is an epistemic theory—it is not about what reality is, but what we know about reality.)
In other words, the electrons, whose hardness characteristic is precisely known to us, have their color characteristic in a state of superposition: their color is neither black nor white nor both nor neither, but is in the state of superposition of black color and white color—the fifth state unknown to classical (Newtonian) physics. This thought experiment, therefore, illustrates the concept of the superposition of states. Whereas in classical physics, a system can be only in one state at any moment in time, in quantum mechanics, the system could be in a superposition of states. For example, if we spin a Chanukah dreidel (top), it will spin either clockwise or counterclockwise, depending on which direction we spun it. In quantum mechanics, a top can be in a superposition of states of spinning clockwise and counterclockwise. In fact, physicists routinely put electrons in the superposition of states of having spin up and spin down, which is roughly equivalent to spinning clockwise and counterclockwise.
This experiment also illustrates the Heisenberg uncertainty principle, according to which, as we have said above, a state where one of the two complementary characteristics has a definite value somehow corresponds with a superposition of many states for the other characteristic thereby making it indefinite.
This is precisely what is going on in the Torah narrative of the Tree of Knowledge! As mentioned above, in quantum physics “color” and “hardness” are just placeholders for any complementary (in math speak, “canonically conjugate”) characteristics. In applying this concept to the Torah narrative, let us replace “color” with the absolute objective truth about right and wrong so that white and black colors represent right and wrong, respectively. Similarly, let us replace “hardness” with “goodness” so that hard and soft correspond to good and evil respectively.
For as long as Adam and Eve were endowed with the intellectual prowess to know right and wrong precisely, the complementary knowledge of good and bad was in the state of superposition—the first humans, before their primordial sin, were ambivalent about good and bad. After the sin, the situation flipped, as in our example with the three boxes above: the knowledge of good and bad that came with the forbidden fruit put the knowledge of right and wrong into the state of superposition. Thus, Adam and Eve could no longer distinguish between true and false, between right and wrong—and with that inability came the loss of Paradise. As we see, the tree of knowledge of good and evil served as the “hardness” box, as it were, in the three-box assembly above, erasing the information about true and false from the minds of Adam and Eve. The Tree of Knowledge thus acted as the quantum eraser. (For mathematically inclined readers and readers familiar with quantum mechanics at least on the introductory level, see the addendum to this chapter for the mathematical treatment of these ideas.)
The Ego and the Loss of Paradise
To be able to discern between true and false, to know right from wrong, is a matter of judgment. It is an intellectual judgment, which does not require and, indeed, does not permit any emotional involvement. A judge must be independent and have no self-interest in the matter at hand. Thus, one’s ego cannot be involved in the process. The problem is that once the ego gets involved, it tends to insert itself into every aspect of one’s life or thoughts. Having an ego, one can no longer objectively decide between right and wrong, because one’s decision-making is tainted by one’s emotional involvement and self-consciousness, by one’s ego.
The knowledge of good and evil, on the other hand, is just the opposite of the knowledge of true and false—it requires emotions and ego. Unlike true and false, which are objective and absolute categories, good and bad are always relative to the person making the judgment—is it good for me? The ego sets the point of reference, with respect to which good and bad are decided. The involvement of the ego necessary to know good and bad precludes the objectivity necessary to know right and wrong—hence the mutual incompatibility. From this point of view, Paradise is a metaphor for the mental state in which one focuses on objective right and wrong rather than subjective good and bad. The change of the perspective from the abstract true and false to the emotional is it good for me, or is it bad for me is a paradigm shift in human consciousness of cosmic proportions—the end of the age of innocence.
After the primordial sin of Adam and Eve, all humans have an ego,[6] and we all lack the intellectual ability to judge right and wrong objectively. If pre-sin clarity was called Paradise, after the sin, Paradise was lost.
It is interesting to note that in all spiritual traditions, the path to spiritual enlightenment and union with the Divine (unio mystica or, in Hebrew, devekut[7]) lies through the practice of asceticism. People who seek honor, power, or base transient pleasure through sexual or other sensory indulgencies have no hope of achieving spiritual enlightenment, which is seen as incompatible with any form of self-gratification.
Commenting on the verse, “and I will take sickness away from the midst of thee” (Exodus 23:25), the Lubavitcher Rebbe, Rabbi Menachem Mendel Schneerson, says,
The sickness mentioned here . . . refers to the source of all sickness, i.e., the feeling of self-consciousness that was caused by the sin of the Tree of Knowledge. Before the sin, there was no concept of self-consciousness, as reflected in the verse: “and they were both naked and they were not ashamed.”[8] The sin led to the feeling of self-consciousness, as reflected in the verse: “and the woman saw that the tree was good to eat.”[9] … The sin of the Tree of Knowledge had an effect on everyone, even on the righteous.[10]
Lessons in Sefer HaMaamorim, Selected Discourses of the Lubavitcher Rebbe
The Rebbe further speaks of four people discussed in the Talmud[11] who died not because of their own sins, but due to the “counsel of the serpent.” The primordial snake injected his poison of egocentrism into all of humanity, and even the best of the best have a minute dose of that poison—the self-consciousness stemming from one’s ego. Even completely righteous people, who are selflessly dedicated to serving God, still have a drop, however small, of that poison from the primordial snake. It has become part of our spiritual and psychological DNA.
Now, perhaps, we can also understand why the prohibition against eating the fruit of the Tree of Knowledge carried the threat of such harsh punishment—death. Before that sin, humans were meant to live forever; there was no inflated ego desiring self-gratification and, therefore, no need for death. That evil was embedded in the fruit of the Tree of Knowledge and was, therefore, external to any human being. Upon tasting the forbidden fruit and internalizing the evil, the first humans inflated their egos and acquired the egotistic desire for self-gratification. This, perhaps, brought about the need for death as a means to rectify the human ego, because death is the ultimate self-nullification (in Hebrew, bitul).
The messianic redemption, which in many ways harkens back to the pre-sin innocent age of Paradise, is seen as the stage in human history after the primordial sin has been atoned for, and the human ego has been rectified to the point that it requires no further nullification, which automatically removes death from the world. The messianic time, therefore, is the stage of Paradise when we return to the state of intellectual enlightenment when we will once again know right and wrong, but not know good and bad. It seems that the uncertainty principle will hold even in messianic times.
Addendum: The Superposition of States
In quantum mechanics, every physical state is described as a vector in Hilbert space. A Hilbert space is an abstract space that is an extension of the familiar Euclidean space on any number of dimensions, including infinitely-dimensional space. A vector is a mathematical object that has a direction and a magnitude, such as an arrow. In quantum mechanics, it is customary to write vectors using Dirac bra-ket notations, where bras and kets are denoted by a combination of a vertical line | and an angular bracket 〉. A bra vector A is denoted as ⟨A|, and a ket vector A is denoted as |A〉. Multiplying a vector by a scalar (a number) just extends the vector’s magnitude without changing its direction: a|A〉 is the same as |aA〉.
Let us now consider a system characterized by a state called “truth.” The truth state has two values: true and false. Thus, its two possible values define vectors in a two-dimensional Hilbert space: |true〉 or |false〉. These vectors could be expressed as columns:

In linear algebra, such a column is also called a single-column matrix or a vector. An operator is a prescription which, acting on a vector in a Hilbert space, transforms this vector into another vector in the same Hilbert space. For example, if |A〉 is a vector in a Hilbert space H, and O is an operator, O|A〉 = |A’〉, where |A’〉 is another vector in H. If an operator O and a vector |A〉 happen to have a relationship such that

where a is any number, |A〉 is called the eigenvector of O, and a is an eigenvalue of O. This relationship, of course, simply means that the length of the vector |A〉 is extended by the factor of a without changing its direction.
We can define a truth operator T as a matrix,

where we agree that “truth = 1” means “true” and “truth = -1” means “false.”
Let us recall from linear algebra the rule for multiplying a 2×2 matrix by a single-column matrix (a vector):
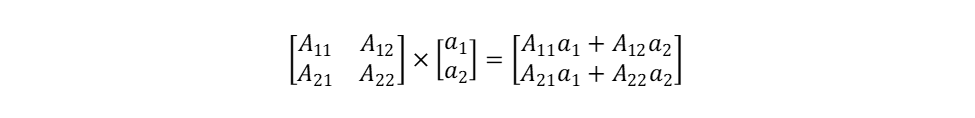
Let us now apply the Truth operator to the vector |true〉:
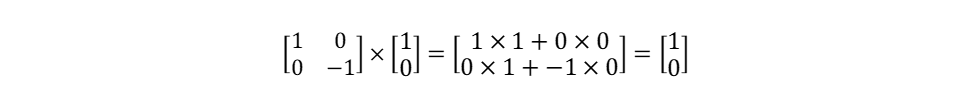
We have, therefore,
T|true〉=1|true〉
Thus, we proved that the vector |true〉 is an eigenvector of the Truth operator T, and truth (recall that truth = 1) is an eigenvalue of the Truth operator T.
The system we defined above as having the state of truth has another state—“goodness.” The “goodness” state also has two values: good and evil (or bad) Thus we can define these values as vectors in the same two-dimensional Hilbert space: |good〉 and |evil〉. In quantum mechanics, two-dimensional Hilbert space is called the spin space (because spin also has two values—up and down). These vectors could likewise be expressed as columns:
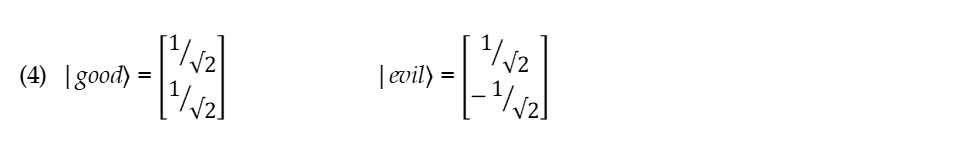
Similarly, let us define a goodness operator G as a matrix,

where we agree that “goodness = 1” means “good” and “goodness = -1” means “evil.”
It is easy to see that |good〉 and |evil〉 vectors happen to be eigenvectors of the goodness operator.
Vectors |true〉, |false〉, |good〉, and |evil〉 are called state vectors because they define the state (collection of properties) of the system under consideration.
Let us recall from vector algebra that if vector A has components a1 and a2, and vector B has components b1 and b2:
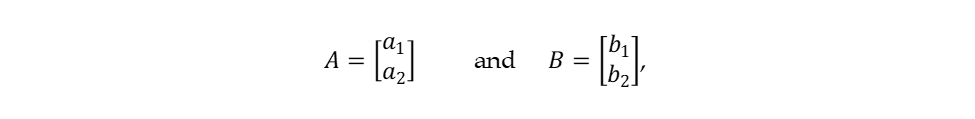
Then
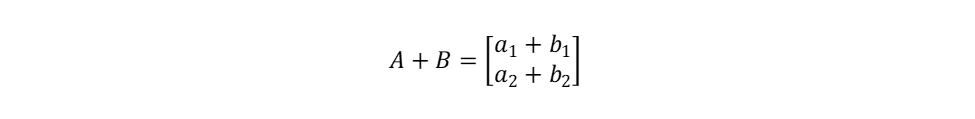
Another rule from vector algebra says that to multiply a vector by a number you need to multiply the components of the vector by that number:

It follows from (1) and (4) that
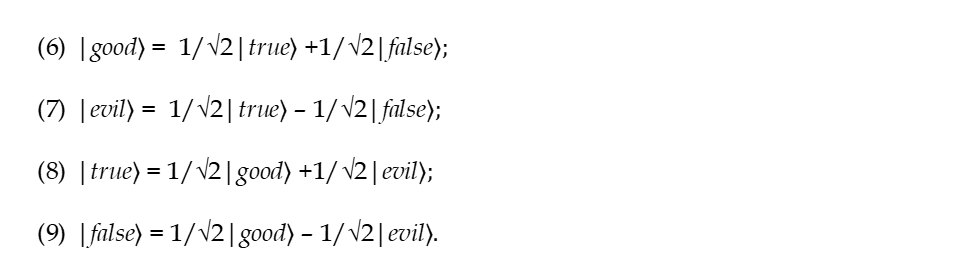
Let us check for example the first of these equalities. To do that, let us calculate the right side of the expression (6):
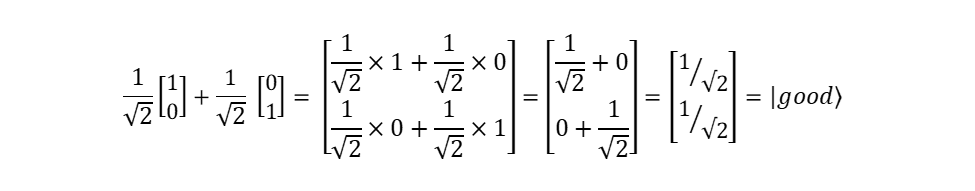
We see that equality (6) is indeed correct. It is just as easy to verify the correctness of the equalities (7)-(9).
To translate these formulas into words:
the equality (6) states that good (|good〉 vector) can be expressed as a linear superposition of true (|true〉vector) and false (|false〉vector);
the equality (7) states that evil (|evil〉 vector) can also be expressed as a linear superposition of true (|true〉vector) and false (|false〉vector);
the equality (8) states that true (|true〉 vector) can be expressed as a linear superposition of good (|good〉vector) and evil (|evil〉vector); and
the equality (9) states that false (|false〉 vector) can also be expressed as a linear superposition of good (|good〉vector) and evil (|evil〉vector).
These formulas express the superposition of states, confirming the Heisenberg uncertainty principle, which states that knowing the precise value of one characteristic puts the complementary characteristic in the state of superposition. To see how these formulas express mathematically the mechanics of the primordial sin of the Tree of Knowledge, let us unpack their meaning.
Let us consider equations (6) and (7), which equates the state vectors |good〉 and |evil〉 to linear combinations of state vectors of |true〉 and |false〉. A linear combination of these vectors means that the system is in the state of superposition of true and false. These two equations say that whenever the goodness state is well defined, i.e., we know exactly what the state vectors |good〉 and |evil〉 look like, the truth state is not defined at all, as it corresponds to the states of superposition of |true〉 and |false〉, as per equations (6) and (7). In mathematical terms, it is expressed in the fact that whereas |true〉 and |false〉 vectors are eigenvectors of the Truth operator T, |good〉 and |evil〉 vectors are not.
Let us now consider equations (8) and (9), which equate the state vectors |true〉 and |false〉 to linear combinations of state vectors |good〉 and |evil〉. These two equations say that whenever the truth state is well defined, i.e., we know exactly what the state vectors |true〉 and |false〉 look like, the goodness state is not defined at all, as it corresponds to the states of superposition of |good〉 and |evil〉, as per equations (6) and (7). Again, in mathematical terms, it is expressed in the fact that whereas |good〉 and |evil〉 vectors are eigenvectors of the Goodness operator G, |true〉 and |false〉 vectors are not.
We see, therefore, that true and false states on the one hand are incompatible with good and evil states on the other—whenever we have a definite state of true or false, we have a superposition of states of good and evil, and vice versa.
This situation is exactly analogous to the pre- and post-sin states of the mentality of Adam and Eve in Paradise. Before tasting from the tree of knowledge of good and evil, they knew exactly what was true and what was false; they knew right from wrong. Their ego did not taint their judgment and, being free from any egotistic desires for self-gratification, they had no concept of good and bad, which for them existed in the abstract state of superposition.
After tasting the forbidden fruit, however, the situation reversed. Having inflated their ego and having acquired the taste of self-gratification, they acquired the knowledge of good (what is good for me) and evil (what is bad for me). Consequently, as Maimonides states in the Guide for the Perplexed, they lost all knowledge of true and false, which went from being well-defined before the primordial sin to an abstract state of superposition after the sin. The information about true and false was erased by the forbidden fruit of the Tree of Knowledge—the quantum eraser. Adam and Eve lost their ability to objectively judge right from wrong.
This metamorphosis is born out by the equations (6)-(9).
We see from the above that our parallels between Heisenberg’s uncertainty principle and the primordial sin according to Maimonides, between the relationship of right and wrong, and good and bad and the superposition of states, between the forbidden fruit and a quantum eraser are not just words but represent precise structural parallels that can be easily described mathematically. One can only marvel at the undeniable fact that these peculiar concepts of quantum physics are encoded in the biblical narrative.
Endnotes:
[1] Rabbi Moshe ben Maimon (a.k.a. RaMBaM) (1138/1135–1204), the most prominent medieval Jewish philosopher and codifier whose exceptional role in Judaism was expressed by the epitaph on his tombstone, “From Moses to Moses, there is no other Moses.”
[2] I am very grateful to my son-in-law, Maimon Kirschenbaum, for bringing this parallel to my attention.
[3] In physics, such pairs of variables are called canonically conjugate variables; examples of such pairings include coordinates and momenta, or time and energy.
[4] The Heisenberg uncertainty principle states: Δx×Δp ≥ ½ћ, where Δx is the uncertainty in the measurement of the position x, Δp is the uncertainty in the measurement of the momentum p, and ћ is the reduced Planck constant h/2π.
[5] See chapter 1 of David Z. Albert, “Quantum Mechanics and Experience” (Harvard University Press, 1992).
[6] The first known use of the word “ego” to mean the self/one’s self-consciousness was in 1789, by Johann Gottlieb Fichte, German idealist philosopher. However, neither Fichte nor Freud with whom this word is mostly associated, invent ego; they were first to talk about it in modern philosophy and psychiatry. The words yesh (“self”) or yeshut (“ego,” “selfhood”) have also been widely used in Jewish thought and particularly in Chasidic philosophy.
[7] The Kabbalistic concept of Devekut, the ecstatic state of “cleaving” to God, is not synonymous with the notion of unio mystica, which in other spiritual traditions means merging with the Divine. In Judaism, a human soul cannot completely unite with God, who remains utterly transcendent and unknowable. The best we can do is to strive to cleave to God by nullifying our ego—bitul.
[8] Genesis 2:25
[9] Genesis 3:6
[10] Lessons in Sefer HaMaamorim, Selected Discourses of the Lubavitcher Rebbe, “Lo Sih’yeh Meshakeila” (New York: Kehot Publication Society, 2015), pp. 168–173.
[11] Talmud, tr. Shabbat, 55b; tr. Baba Batra 17a.
Excellent article. Yasher Koach!
Very nice article. I think that they did not know that eating the fruit was wrong. I think they only knew it was forbidden.