Passover has ended. All Jews hastily return their Passover dishes to storage in special cabinets or the attic until the next Passover. After an eight-day break, home becomes filled with the aroma of freshly baked bread. Passover leaves us with the pleasant taste of burnt matzot, memories of the Seder spent with family, and stories of the Exodus. But did Passover really end?
In the Mishnah (the precursor to Talmud), the holiday of Shavuot (“Pentecost”) is called Atzeret. This word is familiar to us from Shemini Atzeret—the holiday that follows immediately after the seven days of Sukkot, often simply viewed as the last day (or, in the diaspora, the last two days) of Sukkot. Either way, Shemini Atzeret is the conclusion of the festival of Sukkot. By designating Shavuot as Atzeret, the Mishnah seems to imply that it is not so much an independent holiday as it is the conclusion of Pesach (“Passover”), just as Shemini Atzeret is the conclusion of Sukkot.
Let us recall that the main idea of Passover is the idea of freedom, freedom from the bondage of Egyptian slavery. That is why the Passover is called in the liturgy Zeman Cheruteinu (“Time of our Freedom”). G‑d took the Jewish people out of Egypt and made them free. But did they really become free? Sometimes, a slave freed by his master remains in slavery voluntarily because there is no place for him to go, because he does not know any other existence and does not have a purpose in life. So what does this really mean, “freedom”?
In physics, this concept is defined in terms of “degrees of freedom.” Simply put, a degree of freedom is a choice between two alternatives. (Formally, it is an independent parameter of the system.) In mechanics, for example, degrees of freedom represent different possible directions of movement. Thus, a body moving only linearly has one degree of freedom, it has only one choice—to move left or right. If there is another choice—to move up or down—we say that the system has two degrees of freedom. If there is still another choice—to move forward or backward—we say that the system has three degrees of freedom. And so on.
Every degree of freedom can be viewed as a dimension in the so-called phase space. The state of the system can be described as a point in such phase space. Since every point-particle in classical mechanics is fully described by its three coordinates (X, Y, Z) and three velocities (Vx, Vy, Vz) (or, in quantum mechanics, it is customary to describe a subatomic particle by its three coordinates and three components of its momentum), the phase space of a single point-particle has six dimensions (three familiar spatial dimensions plus three additional dimensions representing three components of momentum). A system comprising three particles will have eighteen (6×3=18) dimensions of its phase space. In general, N particles have 6N-dimensional phase space.
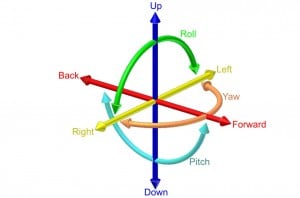
In addition to the translational degrees of freedom, such as moving in three spatial directions, a system can have rotational degrees of freedom, called pitch, roll, and yaw. Rotation around each axis may be clockwise or counterclockwise.
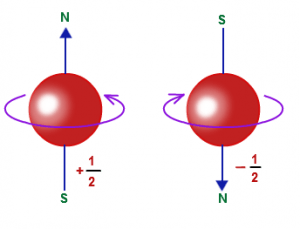
Spin is a quantum-mechanical degree of freedom analogous to angular momentum, although no real rotation is involved. Spin can be pointed down as if corresponding to clockwise “rotation” or up as if corresponding to counterclockwise “rotation” (in reality, no real rotation is associated with spin).
In mechanics, therefore, the number of degrees of freedom is equal to the number of “choices” between alternative possibilities, such as left or right, up or down, forward or backward, clockwise or counterclockwise.
The same is true of man… Our freedom is the freedom to choose between alternative options. Since human beings exist in the physical and spiritual worlds, degrees of freedom also exist in both worlds.
Physical freedom is the freedom to move around, to choose one’s residence, occupation, etc. This freedom is relative and has many levels. Thus, people in the former Soviet Union, for example, were not completely free, since their movement outside and inside the country was limited. At the same time, even there, most people had more freedom than a person who was in jail and could not move beyond the barbed wire. In America, former Soviet emigree acquired more freedom—that’s why it is called the “free world.” However, even here, the choice of residence, if not dictated by the authorities, is determined by the employment, etc. No wonder that, in the free world, only independently wealthy people are considered truly free; their options are not limited by employment, market conditions, etc. Everything is relative.
Freedom in the spiritual (or moral) dimension is the freedom to choose between good and evil. The oldest known book of Kabbalah, Sefer Yetzirah, describes three domains: Olam (“World,” i.e., space), Shanah (“Year,” i.e., time), and Nefesh (“soul,” i.e., the spiritual or moral dimension). The third domain, Nefesh, is described in Sefer Yetzirah as “the depth of good and the depth of evil.” It is this choice between these extreme alternatives that constitutes freedom of choice in the moral dimension. Animals have no spiritual freedom at all because they do not have the ability to choose between good and evil. Moreover, the very concepts of good and evil lose their meaning when there is no choice between them. When a wolf kills a lamb, it does not commit an act of evil, because it has no choice but to follow its instinct. Let us emphasize that freedom is not an opportunity to do what you want (the wolf certainly wants to eat the lamb) but the freedom of choice between alternative possibilities (to eat or not to eat).
Angels do not have freedom of choice either—they can do no evil since their only function is to serve the Creator. (That is evident in the Hebrew word for an angel—malach, i.e., “messenger.”)
Humans are the only creatures in the universe who have freedom of choice in a spiritual sense. Cain killed Abel, but he did not have to kill. His killing of Abel was an evil act because it was an act of free choice. Abraham put up a tent in the desert, which was open on all four sides. He invited weary travelers to take shelter in his tent from the heat of the desert to satisfy their hunger and quench their thirst. An act of hospitality is an act of kindness—an act of goodness—because it is committed voluntarily and not under duress. As we can see, the concepts of good and evil arise when there is a choice, and freedom is the ability to realize this choice. In other words, freedom is always the freedom to choose. And spiritual freedom is the choice between good and evil.
The Kabbalah teaches that the Divine soul (Nefesh Elokit) has 613 aspects—I call them 613 degrees of freedom. As we have said before, freedom is the freedom to choose between alternatives. But what are these alternatives?
After the Jews left Egypt, they obtained physical freedom; they ceased to be slaves. What was lacking, however, were moral alternatives that would result in freedom of the soul. This freedom we have attained at Mount Sinai which is what we celebrate on Shavuot. The freedom we celebrate during Passover is not yet the ultimate freedom. The ultimate freedom came when G‑d gave us the Torah on Mount Sinai. On Passover, we celebrate the freedom from slavery. On Shavuot, we celebrate the freedom of choice between good and evil.
The Torah has exactly 613 commandments—Taryag mitzvoth—one for each aspect of the soul. Now we have moral alternatives: to do a mitzvah or to transgress it. These 613 moral choices have liberated our souls. It was on Mount Sinai that we received 613 degrees of freedom, thereby obtaining our ultimate freedom in the spiritual dimension. It is this spiritual freedom that we celebrate on Shavuot—the giving of the Torah, which completes the physical freedom we celebrated during Passover.


Hi Alexander,
That was a really fantastic post. Can I ask you to clarify something. As you stated, freedom is a function of choice, the ability to choose alternatives. Why is being involved in Torah an important ingreident in choice and freedom? The mishna says eyn lecha ben chorim ela mi sheosek batorah? Why is freedom (ie choice) a necessary function of esek batorah? Doesn’t someone who is not involved in Torah also have moral choice (and hence freedom)?