И говорил он [Авраам] с ними, говоря: «…Послушайте меня и попросите за меня Ефрона, сына Цохара. Чтобы он отдал мне пещеру Махпела (Двойную), которая принадлежит ему, которая находится в конце его поля…» (Бытие 23:8-9)
Двойная: Дом с верхним этажом над ним. Другое толкование: потому что она была удвоена парами (Эр. 53а) (Раши на Бытие 23:9)
В главе Торы Хаей Сара Авраам покупает двойную пещеру, Махпела, в качестве родового захоронения. Почти все классические библейские комментаторы интерпретируют Махпела (то есть «двойная») как пещеру с двумя камерами. Раши придерживается совершенно иного подхода и утверждает, что пещера была известна двухэтажным домом, построенным на ней. Таким образом, слово Махпела относится не к самой пещере, а к дому, построенному на ней. Еще более странно то, что Раши предлагает альтернативное толкование, говоря, что слово «двойная» может также относиться к парам патриархов, которые там похоронены — Адаму и Еве, Аврааму и Саре, Исааку и Ревекке, и Иакову и Лии. Какова связь между этими двумя очень разными интерпретациями?
В физике есть глубокая тайна. Хотя она прямо перед глазами, вы не найдете никакого упоминания о ней ни в одном учебнике физики; вы не услышите, чтобы какой-либо профессор упоминал об этом на лекции (я упоминал, но я никогда не слышал, чтобы кто-то еще говорил об этом). Вам даже не нужно иметь докторскую степень по физике, чтобы понять это – любой ученик старшей школы, изучающий ньютоновскую механику, должен быть в состоянии понять это. Вот она.
Второй закон Ньютона гласит, что для любого тела:
a × m = F, или a = 1/m × F,
где a — это ускорение тела, m — это масса тела, и F — это общая сила, действующая на тело. По сути, второй закон Ньютона гласит, что ускорение a тела с массой m пропорционально силе F, действующей на тело (здесь жирным шрифтом обозначены векторы, то есть величины, которые имеют как величину, так и направление; скорость, ускорение и сила являются векторами, тогда как масса является скаляром — величиной без направления).
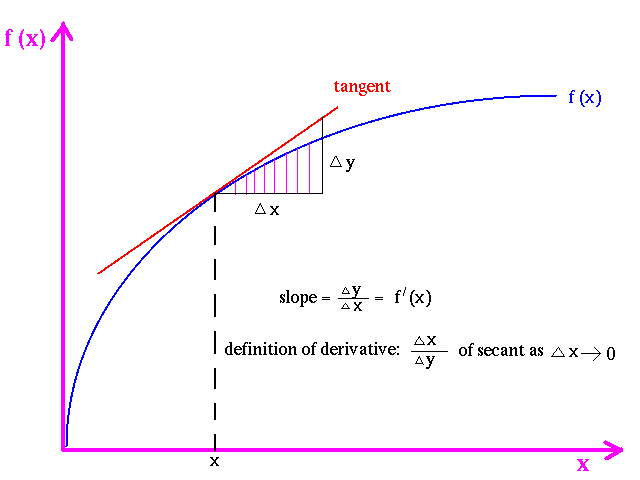
Где же тайна, спросите вы? Для этого нам понадобится немного математики. Скорость объекта — это первая производная положения объекта в пространстве по времени: v = dx/dt.
Проще говоря, производная измеряет чувствительность к изменению значения функции (выходного значения) по отношению к изменению ее аргумента (входного значения). Производная функции — это наклон касательной к графику функции в этой точке.
Дом, построенный на поверхности земли, также касается поверхности:

Ускорение — это скорость скорости, то есть производная скорости по времени: a = dv/dt.
Это делает его второй производной (производной производной) положения по времени: a = d2x/dt2.
Производная функции — это скорость, с которой эта функция изменяется с изменением аргумента. Сама производная является функцией — математической структурой, которую мы строим поверх исходной функции. Поскольку это функция сама по себе, мы можем взять производную от этой функции — вторую производную исходной функции и построить еще одну структуру «поверх» исходной функции, «верхний этаж» над ней. Таким образом, метафорически говоря, вторую производную можно рассматривать как двухэтажную структуру, возведенную поверх исходной функции.
Вторая производная появляется повсюду в физике и, кажется, представляет собой фундаментальный закон динамики.

Во время своей нобелевской речи физик Юджин Вигнер сказал, что роль науки состоит в том, чтобы отделять закономерности от шума. Это было одно из самых проницательных заявлений, которые я слышал о природе науки. Это то, что Ньютон сделал со своим Вторым законом.
Представим себе, что мы живем до Ньютона и пытаемся изучить движение объекта. Мы бы наблюдали такое движение много раз, отмечая соответствие между положением объекта и временем, в которое это положение измеряется. В конце длительного эксперимента мы накопили бы большой объем данных — точек на графике, отображающем положение объекта с течением времени. Мы могли бы представить, что некоторые из этих данных являются случайными (то есть шумом), а некоторые представляют собой некоторую закономерность — еще неизвестный закон физики. Все динамические процессы в физике описываются дифференциальными уравнениями (такими как Второй закон Ньютона). Если бы мы предположили, что наша неизвестная закономерность описывается дифференциальным уравнением первого порядка (первой производной), чтобы решить его, нам пришлось бы интегрировать, поскольку интеграл является противоположностью производной. Однако производная константы всегда равна нулю, что означает, что когда мы обращаем операцию дифференцирования, беря интеграл, мы можем знать ответ только с точностью до константы. Это означает, что если наша закономерность описывается дифференциальным уравнением первого порядка (первой производной), у нас будет слой случайного шума, представленный константами, появляющимися во время интегрирования. Чтобы избавиться от них, нам нужно выбрать начальные условия. В случае движущегося объекта нам нужно знать начальное положение объекта.
Если, однако, наша закономерность описывается дифференциальным уравнением второго порядка (второй производной), чтобы решить его, нам нужно интегрировать дважды, получив два набора констант и, следовательно, два слоя случайного шума. Чтобы избавиться от этого шума, нам нужно знать два набора начальных условий. В случае движущегося объекта нам нужно знать его начальное положение и начальную скорость.
Гений Ньютона заключался в том, чтобы догадаться, что фундаментальным законом механики (и, как выяснилось позже, динамики в целом) является дифференциальное уравнение второго порядка (вторая производная). Вот почему в механике, чтобы предсказать будущее положение объекта в какой-то момент времени, нам нужно знать его начальное положение и скорость — нам нужна пара начальных условий. В математике начальные условия являются прародителями будущего значения функции — «патриархами», если бы это было так.
Теперь все части головоломки складываются вместе: структура со вторым этажом поверх пещеры в первой интерпретации Раши является метафорой второй производной — структуры второго этажа, которую мы строим поверх исходной функции. Пары, похороненные в пещере, относятся к паре начальных условий, необходимых для решения уравнения со второй производной.
Хотя вторые производные повсеместно встречаются в физике, я всегда думал, что это универсальный принцип. По какой-то причине, всякий раз, когда мы хотим изучить эволюцию динамической системы во времени, оказывается, что именно вторая производная представляет собой закономерность с двумя слоями случайного шума, связанными с ней.
Вот почему попытки подогнать кривую к прошлому поведению рынка, чтобы предсказать будущие цены на акции, — это пустая трата времени — вы будете смешивать закономерности с шумом. Вы можете предсказать будущую цену акций (или цену любого товара или финансового инструмента), рассматривая вторую производную цены по времени. Если вы хотите разбогатеть, я только что рассказал вам, как это сделать.
Даже в медицине, когда мы сдаем анализы, важна не столько текущая величина анализа, сколько то, как он «ускоряется» во времени, то есть вторая производная. Действительно, в одном исследовании значимости ПСА в качестве прогностического маркера рака предстательной железы исследование показало, что именно вторая производная — ускорение роста ПСА — имела наибольшую прогностическую ценность. Действительно, вторая производная рулит! Это не означает, что статические тесты, показывающие снимок во времени, бесполезны. Но если мы сможем часто повторять тест и вычислять вторую производную, это даст нам гораздо большую диагностическую ценность.
Возможно, Раши намекал нам на этот секрет, объясняя значение слова Махпела как двухэтажную структуру поверх пещеры.