Фрактальные узоры в Торе

В разделе Торы Эмор (Левит 21:1–24:23) нам предписано воздерживаться от работы каждый седьмой день в Шаббат. Раздел Торы следующей недели, Бегар, продолжает эту тему и предписывает нам воздерживаться от сельскохозяйственных работ каждый седьмой субботний год, Шмита. И Тора на этом не останавливается. Она предписывает нам отсчитать семь Шмит, а затем соблюдать Юбилей, Йовель.

Вы замечаете закономерность? Каждые семь дней, каждые семь лет, каждые семь Шмит… Кроме того, Мидраш утверждает, что мир будет существовать семь тысяч лет, причем седьмое тысячелетие будет тысячей лет царства Машиаха (Мессии) — йом шекулой Шаббат — один долгий Шаббат. Мудрец второго века, раввин Хуния бен Хакана, интерпретирует этот Мидраш как означающий, что мир продлится семь Космических Шмит, то есть 49 тысяч лет (что, согласно выдающемуся каббалисту 13–14 веков Рб. Исааку из Акко, говорит не о земных годах, а о небесных годах, которые эквивалентны примерно 15 миллиардам лет — что недалеко от текущей оценки космологического возраста Вселенной в 13,8 миллиарда лет, но это уже другая тема).

Общим здесь является самоподобие в разных масштабах — число семь играет роль периода в многомерной спирали с несколькими периодами: семь дней, семь лет, семь шмитит (строго говоря, семь шмит плюс один, так как Юбилей приходится на каждый 50-й год), семь тысячелетий, семь Космических Шмит… В математике такие закономерности называются фракталами. Фрактал, по определению, — это закономерность, которая повторяется в каждом масштабе. Это свойство называется самоподобием.

Фрактальная геометрия — это увлекательная и относительно новая область математики. Вот некоторые из самых простых примеров фрактальных множеств:

Канторово множество. Чтобы построить Канторово множество, мы сначала рисуем линию. Мы делим эту линию на три сегмента и удаляем средний сегмент. Мы продолжаем эту процедуру до бесконечности. Вот Канторово множество для семи итераций:

Снежинка Коха. Снежинку Коха можно построить, начав с равностороннего треугольника, а затем рекурсивно изменяя каждый отрезок линии следующим образом:

1. Мы делим отрезок линии на три сегмента равной длины.
2. Затем мы рисуем равносторонний треугольник, у которого средний сегмент из шага 1 является его основанием и направлен наружу.
3. Наконец, мы удаляем отрезок линии, который является основанием треугольника из шага 2.

Мы повторяем этот процесс до бесконечности. Нельзя не заметить, что вторая итерация алгоритма создает Звезду Давида, Маген Давид. Удивительное свойство снежинки Коха заключается в том, что она имеет конечную площадь, ограниченную бесконечно длинной линией.

Треугольник Серпинского. Этот фрактал представляет собой равносторонний треугольник, рекурсивно подразделенный на более мелкие равносторонние треугольники.

Он построен путем удаления треугольных подмножеств:

1. Начнем с равностороннего треугольника.
2. Мы делим его на четыре меньших равносторонних треугольника и удаляем центральный.
3. Затем мы повторяем шаг 2 с каждым из оставшихся меньших треугольников и так далее.

Ковер Серпинского:

Ковер Серпинского очень похож на Треугольник Серпинского, где вместо треугольников мы используем квадраты:

Фрактальный полог. Фрактальный полог имеет следующие три свойства:

1. Угол между любыми двумя соседними отрезками линии одинаков по всему фракталу.
2. Отношение длин любых двух последовательных отрезков линии постоянно.
3. Точки в самом конце самых маленьких отрезков линии взаимосвязаны.

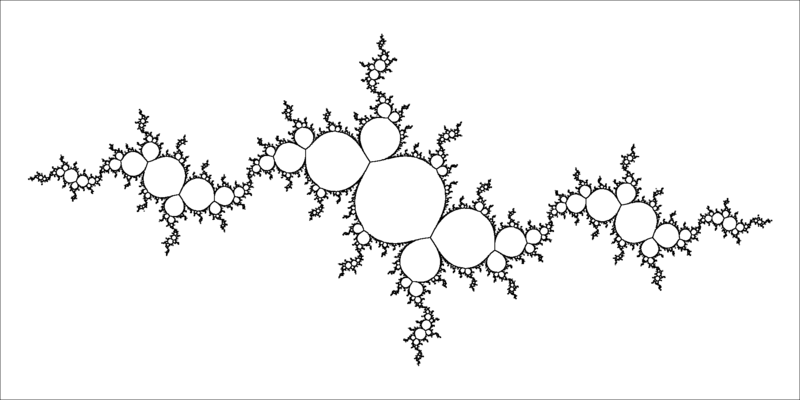
Общей нитью всех этих изображений является самоподобие в каждом масштабе. Некоторые фракталы гипнотически красивы. Взгляните, например, на этот фрактал множества Жюлиа:

Фрактальные формы существуют не только в математике, но и повсюду вокруг нас. Еврейский математик Бенуа Мандельброт заметил, что большая часть природы имеет фрактальную форму — будь то кленовый лист, цветная капуста, горы, береговая линия, легкие или кровеносные сосуды — все они имеют одно общее свойство, самоподобие в различных масштабах. (Несколько лет назад я предположил, что наше пространство-время, будучи гладким в большом масштабе, должно быть фрактальным в микромасштабе. Если это правда, то эта фрактальная «шероховатость» в малом масштабе может позволить преодолеть разрыв между общей теорией относительности и квантовой теорией поля.) Фракталы повсеместны в природе. Почему это так?

Мне кажется, что причина этого кроется в структуре сфирот в мире Тикун (Исправление). Сфирот — божественные эманации, которые являются «строительными блоками» творения, — являются основополагающей концептуальной основой всего творения. В то время как в мире Тогу (Хаос) сфирот разъединены, что привело к швират гакелим (разбиение сосудов), в мире Тикун они взаимовключены, то есть каждая сфира включает в себя все десять сфирот. Таким образом, Хохма включает в себя все десять сфирот: Хохма из Хохмы, Бина из Хохмы, Даат из Хохмы, Хесед из Хохмы, Гвура из Хохмы, Тиферет из Хохмы, Нецах из Хохмы, Ход из Хохмы, Йесод из Хохмы и Малхут из Хохмы. Десять сфирот разветвляются на 100 комбинаций. Сейчас мы находимся в днях отсчета Омера, когда каждый день мы исправляем определенную комбинацию из семи мидот (семь нижних сфирот), считая Хесед из Хеседа, Гвура из Хеседа и т. д. — всего 49 перестановок. Каждая из 100 комбинаций, в свою очередь, дополнительно включает в себя каждую из десяти сефериот, что приводит к дальнейшему разветвлению сфиротического дерева, до бесконечности. Это идеальная фрактальная структура. Неудивительно, что физический мир, отражая свое духовное происхождение, демонстрирует аналогичные фрактальные закономерности. В то время как природа предоставляет множество примеров фрактальных закономерностей в пространстве, Тора показывает нам уникальную фрактальную закономерность во времени и в духовной сфере.

Еще одна фрактальная закономерность, уникальная для Торы, обнаруживается в одном из инструментов библейской герменевтики — гематрии. В иврите числа записываются с использованием букв Алеф Бет: 1 — это Алеф, 2 — это Бет и т. д. Таким образом, каждая буква иврита имеет числовое значение, гематрию. Самый простой способ вычислить гематрию еврейского слова — это сложить числовые значения всех букв, составляющих это слово. Например, слово ахад (один) пишется Алеф-Хет-Далет. Числовые значения этих букв: Алеф=1, Хет=8 и Далет=4. Таким образом, гематрия ахад равна 1+8+4=13. Однако у каждой буквы есть свое название и, следовательно, своя гематрия: Алеф пишется Алеф-Ламед-Пе, поэтому его гематрия равна 1+30+80=111. Хет пишется Хет-Йуд-Тав, поэтому его гематрия равна 8+10+400=418. Далет пишется Далет-Ламед-Тав, поэтому его гематрия равна 4+30+400=434. Расширение каждой буквы слова ахад с написанием каждой буквы дает Алеф-Ламед-Пе-Хет-Йуд-Тав-Далет-Ламед-Тав, поэтому расширенная гематрия ахад равна 111+418+434=963. Такая гематрия называется милуй (заполненной). Каждая буква в расширенном, милуй, написании может, в свою очередь, быть записана снова, до бесконечности. И снова у нас есть фрактальный узор.

Вся герменевтика Торы носит фрактальный характер. Существует пять уровней толкования Торы, называемых по их аббревиатуре, Пардес (сад):

1. Пшат (буквальное значение)
2. Ремез (намек)
3. Драш (гомилетика)
4. Сод («секрет» — Каббала)
5. Сод шеб’Сод («Секрет секретов» — Хасидут)

В свою очередь, каждый из этих уровней также имеет пять уровней, так что у нас есть Пшат из Пшата, Ремез из Пшата и т. д. — фрактальная структура.

В более широком масштабе Г-дь создал мужчину и женщину по Своему образу. Он также повелел им размножаться. Это привело в движение постоянно растущее, постоянно разветвляющееся дерево человечества. Как объяснил Бенуа Мандельброт, фрактал — это «форма, обладающая тем свойством, что каждую небольшую часть можно рассматривать как уменьшенную масштабную копию целого». Глядя на человека, каким бы маленьким он ни был, мы никогда не должны забывать, что это миниатюрная копия Г-да. Давайте проявим немного уважения!