מחזה היקום נעשה כה גדול יותר, כה יפה יותר, ראוי יותר ליוצרו, כאשר יודעים שמספר קטן של חוקים, שנקבעו בחוכמה רבה, מספיקים לכל התנועות.
פייר לואי מופרטואי (1744)
מבין החוקים הפחות או יותר כלליים, שגילוים מאפיין את התפתחות המדע הפיזיקלי במאה האחרונה, עקרון הפעולה המינימלית הוא כיום בוודאי זה אשר, בצורתו ובהיקפו, ניתן לומר שהתקרב ביותר למטרה האידיאלית של החקירה התיאורטית. משמעותו, כאשר מבינים אותה כראוי, מתפשטת לא רק לתהליכים מכניים, אלא גם לבעיות תרמיות ואלקטרודינמיות. בכל ענפי המדע שבהם הוא חל, הוא נותן לא רק הסבר למאפיינים מסוימים של תופעות הנתקלות כיום, אלא מספק כללים שבאמצעותם ניתן לקבוע באופן מלא את השינויים שלהן בזמן ובמרחב. הוא מספק את התשובות לכל השאלות הקשורות אליהן, בתנאי שהקבועים הנחוצים ידועים והתנאים החיצוניים הבסיסיים נבחרו כראוי.
מקס פלאנק (1909)
תוכן העניינים
II. מבוא לעקרון הפעולה המינימלית <— אתה כאן
VII. V. המקור הרוחני של עקרון הפעולה המינימלית
זהו הפרק השני בסדרה על עקרון הפעולה המינימלית. בפרק הראשון, “עקרון הפעולה המינימלית I“, הוכרנו לטלאולוגיה. למדנו שטלאולוגיה היא סיבה או הסבר למשהו המשמש כפונקציה של מטרתו, בניגוד למשהו המשמש כפונקציה של הסיבה שלו. נחשב כבעל מטרה, יעד או קצה שאליו הם שואפים. המטרה הסופית נקראת הסיבה הסופית (causa finalis). למדנו גם שהיהדות היא ללא ספק טלאולוגית עד הלב וכי האמונה היהודית מבוססת על האמונה באלוקים בעל מטרה, שברא עולם בעל מטרה. בפרק זה (השני), אנו הולכים לקבל מבוא אינטואיטיבי לעקרון הפעולה המינימלית.
II. מבוא לעקרון הפעולה המינימלית
1. מזעור פעולה
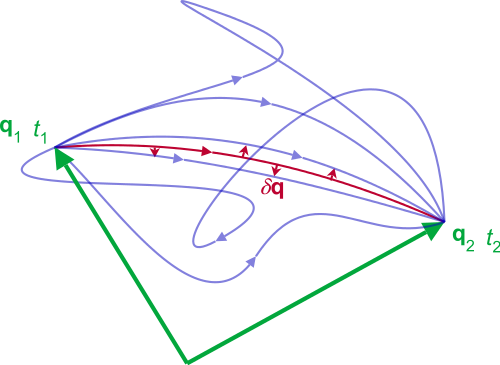
עקרון הפעולה המינימלית ניתן להבנה בקלות. נניח שיש לנו חלקיק בנקודה A בזמן T1 ובנקודה B בזמן T2. השאלה שאולי נרצה לשאול היא, איך הגיע החלקיק מנקודה A לנקודה B? במילים אחרות, מה הייתה המסלול שלו?
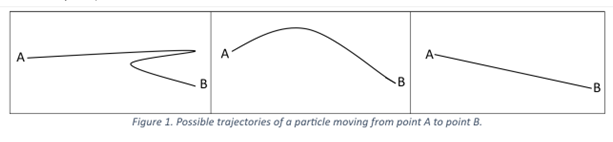
על פי המתכון שמספק עקרון הפעולה המינימלית, אנו מייחסים מספר (הנקרא “פעולה”) לכל עקומה ובוחרים את העקומה עם המספר הקטן ביותר—זהו המסלול הפועל שבו נע החלקיק. בין שלוש הדוגמאות הנתונות לעיל באיור 1, לקו הישר הימני ביותר יש את המספר הקטן ביותר (פעולה) והוא, למעשה, מסלול החלקיק. בניסוח הראשון של עקרון הפעולה המינימלית, הוגדר שלקו הישר יש את הפעולה הקטנה ביותר (המספר הקטן ביותר הקשור אליו). זה נקרא עקרון המרחק המינימלי. מאוחר יותר, הוא הוחלף בנתיב המהיר ביותר—המסלול שלקח את הזמן הקצר ביותר לנסיעה ולכן נקרא עקרון הזמן המינימלי (עקרון פרמה). הניסוח המודרני מתייחס להפרש בין אנרגיה קינטית (אנרגיית התנועה) ואנרגיה פוטנציאלית (למשל, האנרגיה הפוטנציאלית של משיכה כבידתית). אבל עוד על כך מאוחר יותר. כעת, אנו רוצים לפתח אינטואיציה לעקרון האוניברסלי החשוב ביותר הזה.
הבה נציין שבאמצעות עקרון הפעולה המינימלית, אנו יכולים לבחור נכון את המסלול שעבר החלקיק בהתבסס על ערך הפעולה המינימלית הקשור למסלול זה. הבחירה הזו נעשית ex post facto כאשר אנו כבר יודעים את מיקום החלקיק (B) בזמן T2. אבל איך יודע חלקיק לאן הוא יגיע כדי לבחור את הנתיב הנכון? איכשהו, הוא יוצא מיד בנתיב הנכון a priori, כאילו הוא ידע את נקודת היעד—הסיבה הסופית—שהוא מושג טלאולוגי ברור.
עקרון הפעולה המינימלית קובע שכל מערכת מתפתחת בזמן כך שפרמטר מסוים (“פעולה”, הקשורה לאנרגיה) של המערכת ממוזער.[1] זה נראה פשוט באופן מטעה:
δS = 0
כאן S הוא הפרמטר שאנו מנסים למזער, הנקרא פעולה.[2] כפי שהוזכר לעיל, אנו מייחסים ערך S לכל המסלולים האפשריים של עצם נע (אם אנחנו מדברים על מכניקה) ובוחרים מסלול כזה שעבורו S הוא הקטן ביותר—הוא ממוזער או ממוקסם (מוקצן).
נפרק את משמעות הפעולה מאוחר יותר. אבל ראשית, הבה נציין את הטבע הטלאולוגי של חוק חשוב זה—כל מערכת פיזיקלית מתפתחת כך שמטרה מסוימת שנבחרה a priori—הקצנת פעולה—מושגת.
2. הטבע יעיל
בלב עקרון הפעולה המינימלית נמצא רעיון פשוט באופן מפתיע: הטבע יעיל. יתרה מכך, הוא יעיל באופן מקסימלי.
הבה נמחיש עקרון זה עם דוגמה יומיומית.
דמיין שאתה נכנס לפארק, ואתה רוצה להגיע לקצה הנגדי. ישנם נתיבים רבים שאתה יכול לקחת. אתה יכול ללכת בקו ישר ישירות לכיוון סוף הפארק. אתה יכול לקחת דרך עוקפת, לסטות הצידה לפני שפונה לקצה השני. אתה יכול להסתובב במעגלים קצת לפני שפונה לקצה השני. כל נתיב מביא אותך ליעד שלך אך דורש כמויות שונות של מאמץ. הנתיב הראשון הוא הישיר ביותר ודורש הכי מעט הליכה. שאר הנתיבים לוקחים זמן רב יותר ודורשים יותר אנרגיה כיוון שאתה מסתובב יותר.
בגדול, עקרון הפעולה המינימלית אומר שמערכות פיזיקליות מתנהגות כמו אדם יעיל: זה “רוצה” לעבור מנקודה A לנקודה B בדרך היעילה ביותר—כלומר, על ידי שימוש במינימום אנרגיה. הפעולה (הפרמטר שאנו ממזערים) בעקרון זה היא מדד ל”מאמץ” שהמערכת צריכה להשקיע כדי לעקוב אחר נתיב מסוים, תוך התחשבות גם באנרגיה הקינטית שלה (אנרגיה בשל תנועה) וגם באנרגיה הפוטנציאלית שלה (אנרגיה בשל מיקום).
אז, בדיוק כפי שאנחנו עלולים לבחור את הנתיב הקצר ביותר במעבר הפארק כדי לחסוך באנרגיה שלנו, מערכת פיזיקלית “בוחרת” את הנתיב שממזער את הפעולה שלה.
כמובן, זוהי דרך פשוטה להסתכל על זה. אבל הרעיון הבסיסי הוא שהטבע לוקח את נתיב המאמץ המינימלי—הנתיב היעיל ביותר שממזער פעולה. שוב, השגת היעילות הזו היא מטרה טלאולוגית שנבחרה a priory.
מושג זה הוא אינטואיטיבי למישהו המאמין שהקדוש ברוך הוא ברא את העולם. הקדוש ברוך הוא מושלם מכל בחינה, כולל היותו יעיל לחלוטין בבריאת העולם. לפיכך, בריאתו גם היא יעילה (ככל שאפשר במסגרת המגבלות של העולם הפיזי), כיוון שהיא משקפת את תכונות הבורא שלה.
3. עקרון אופטימיזציה
אנו יכולים גם לראות את עקרון הפעולה המינימלית כעקרון אופטימיזציה. מנקודת מבט זו, עקרון הפעולה המינימלית בוחר את הנתיב האופטימלי ביותר. כל תא חי עובד לבצע אופטימיזציה (או איזון) של ריכוז אלמנטים מסוימים (למשל, נתרן ואשלגן) להשגת הומאוסטזיס. הוא עושה זאת על ידי ניסוי וטעייה דרך מנגנוני משוב שונים. כפי שציין המייסד של הקיברנטיקה, נורברט וינר, כל מנגנוני המשוב הם בהכרח טלאולוגיים.
כל חברה שמוכרת מוצר מנסה לבצע אופטימיזציה של מחיר המוצר—ככל שהמחיר גבוה יותר, כך הרווח גבוה יותר. מצד שני, ככל שהמחיר גבוה יותר, פחות אנשים יכולים להרשות לעצמם את המוצר. מה האיזון האופטימלי כך שהמחיר נמוך מספיק כדי להיות זמין לרוב הלקוחות שרוצים לקנות את המוצר אבל גבוה מספיק כדי לשמור על רווח בריא? בכלכלה, פעילות איזון זו מתוארת על ידי עקומת ביקוש. באופן כללי, שווקים פועלים על ידי איזון ביקוש והיצע, וזה נעשה דרך ניסוי וטעייה.
הפיזיקה גם מבצעת אופטימיזציה של האיזון בין אנרגיות קינטיות ופוטנציאליות על ידי בחירת הנתיב שעבורו הפעולה היא מינימלית (או מקסימלית—באופן כללי, קיצונית). עם זאת, המערכת הפיזיקלית לא זקוקה לניסוי וטעייה—איכשהו, היא בוחרת את הנתיב האופטימלי ab initio—מההתחלה.
בדוגמה הקודמת, עקרון הפעולה המינימלית הוצג במונחים של יעילות. אופטימיזציה דומה אבל מושג כללי יותר. אם אנחנו בוחרים לבצע אופטימיזציה של התפתחות המערכת הפיזיקלית כדי למקסם את יעילות האנרגיה שלה, אז זה הופך לנתיב האופטימלי.
אופטימיזציה היא תמיד פעילות איזון. תאים מאזנים את ריכוז הנתרן והאשלגן; שווקים מאזנים היצע וביקוש; ומערכות פיזיקליות מאזנות אנרגיה קינטית ופוטנציאלית. עם זאת, מערכות פיזיקליות מאזנות זאת ללא איזון—הנתיב שלהן מאוזן מההתחלה כאילו הן יודעות איך לעשות זאת. האם זה לא מדהים?
שוב, הבה נשים לב לטבע הטלאולוגי של עקרון הפעולה המינימלית. כל מערכת פיזיקלית בוחרת נתיב לבצע אופטימיזציה של תנאים מסוימים a priori—מזעור (או הקצנת) פעולה. אם תהיתם מדוע הפרק הראשון של סדרה זו הוקדש לטלאולוגיה, אני מקווה שעד עכשיו השאלה שלכם נענתה.
מנקודת מבט תיאולוגית, אין כאן הפתעות. הנביא אמר:
עמדו על דרכים וראו ושאלו לנתיבות עולם איזה דרך הטוב ולכו בה, ומצאו מרגוע לנפשכם.
ירמיהו ו:טז
הנביא קורא לנו להעריך נתיבים שונים ולבחור את הנתיב האופטימלי—”הדרך הטוב”, בדיוק כפי שחלקיק בוחר את הנתיב האופטימלי על פי עקרון הפעולה הנייח שנרמז בפסוק במילה “מרגוע”.
יתרה מזאת, אלוהים הוא ישות מוחלטת ומושלמת, מה שאומר שכל מה שאלוהים עושה, הוא עושה באופן אופטימלי. אין פלא, אם כן, שיצוריו—בני אדם או דוממים—מתנהגים באופן דומה לזה שבו הם נוצרו—הדרך האופטימלית.
כעת, לאחר שיש לנו הבנה בסיסית ותחושה אינטואיטיבית לעקרון הפעולה המינימלית, נוכל לצלול עמוק יותר. בפרק הבא, נכסה את ההתפתחות ההיסטורית של עקרון הפעולה המינימלית.
הטבע יעיל
לקחת את הנתיב הקצר ביותר.
הוא עוקב אחר יודע־כל,
שמלמד את הטבע מתמטיקה.
הוא חסכני, והוא אופטימלי
לבחור את המסלול המהיר ביותר.
מכל המסלולים האפשריים,
הפעולה הוא מחשב.
הפעולה חייבת להיות מותאמת—
נמנעת מכל זרימה,
הבורא חייב להיות מוכר
כמחבר החוק הזה.
הערות שוליים:
[1] במובן המדויק, פרמטר זה מצטמצם או מתמקסם—מתקצן—אך לרוב, הוא מצטמצם, וזו הסיבה שעקרון זה נקרא לעתים קרובות עקרון הפעולה המינימלית. עוד על כך בהמשך.
[2] האות היוונית δ (“דלתא”) פירושה וריאציה. היא דומה לנגזרת בחשבון דיפרנציאלי. כאשר אנו רוצים למצוא מינימום או מקסימום (קיצון) של פונקציה, אנו לוקחים נגזרת של הפונקציה. בכל מקום שבו הנגזרת היא אפס, בנקודה זו, הפונקציה נמצאת בערך הקיצוני שלה (מינימלי או מקסימלי). באופן דומה, כאשר עוסקים בפונקציונלים (פונקציה של פונקציות), אנו משנים אותם כדי לראות היכן הווריאציה היא אפס—זה בוחר פונקציה שהיא מינימלית או מקסימלית ביחס לפרמטר מסוים.