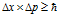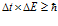עַל-פִּי שְׁנַיִם עֵדִים, אוֹ שְׁלֹשָׁה עֵדִים–יוּמַת הַמֵּת; לֹא יוּמַת, עַל-פִּי עֵד אֶחָד. (דברים יז:ו)
כתבתי על עדים בפוסט הקודם שלי שנקרא בדמיון עדים. ספר דברים חוזר על מצוות רבות שהוצגו קודם לכן, ולכן הוא נקרא גם משנה תורה – חזרה על התורה – פרשת שופטים חוזרת על דין העדים שהוצג לראשונה בספר במדבר, בפרשת מסעי. לכן נחזור לנושא המרתק הזה.

א. נאשם פלילי וחתול שרדינגר
רוב הפושעים בארה”ב מורשעים על סמך ראיות נסיבתיות. נדיר המקרה שבו חבר מושבעים שומע עד ראייה. לדוגמה, רוב הראיות נגד טימותי מקווי היו נסיבתיות. פרופסור למשפטים מאוניברסיטת מישיגן, רוברט פרכט, העיר על משפטו של מקווי, “ראיות נסיבתיות יכולות להיות, ולעתים קרובות הן, חזקות יותר מראיות ישירות.” מבחינה לוגית, זה הגיוני מאוד. אכן, אנשים משקרים בכוונה או עושים טעויות תמימות. “אקדח מעשן”, טביעות אצבעות וראיות DNA הן דוגמאות לראיות נסיבתיות אובייקטיביות שלעתים קרובות יש להן משקל רב יותר בתודעתם של מושבעים הדנים באשמתו של נאשם פלילי מאשר עדותו של עד ראייה שאמינותו ניתנת לערעור בקלות. כתוצאה מכך, תובעים רבים מעדיפים להסתמך על ראיות נסיבתיות. לא כך בדין היהודי. כפי שהתורה מלמדת אותנו בפרשה זו, רק על פי עדות של עדי ראייה יכול בית דין יהודי להרשיע נאשם פלילי. זה לא קל להבנה. האם אין זה אומר שרוב הפושעים יוצאים לחופשי? אולי כן… אבל את ההיגיון של התורה ניתן להבין בקלות מנקודת המבט של מכניקת הקוונטים (QM).
ב-QM חלקיק או מכלול של חלקיקים מתואר על ידי פונקציית גל המצייתת למשוואת שרדינגר. פונקציית הגל (או, ליתר דיוק, ריבוע האמפליטודה של פונקציית הגל) מתארת את ההסתברות למצוא חלקיק באזור נתון של מרחב הפאזה. במילים אחרות, פונקציית הגל אינה חוזה ערכים מדויקים למאפיינים פיזיקליים של החלקיק – אלא רק התפלגות הסתברות למציאת ערכים מסוימים סבירים יותר מאחרים. עם זאת, כאשר אנו מודדים מערכת קוונטית-מכנית, נניח את מיקומו של חלקיק תת-אטומי, אנו תמיד מקבלים ערך מדויק למאפיין שאנו מודדים. כאילו שהתפלגות ההסתברויות או “ענן” ההסתברות פתאום קורס לערך יחיד. ב-QM, זה מכונה קריסת פונקציית הגל. הבעיה היא שקריסה זו של פונקציית הגל אינה נובעת ממשוואת שרדינגר או מכל עיקרון אחר של ה-QM. זה כלל לא חזוי על ידי ה-QM ונוסף אד הוק כדי להסביר ממצאים ניסויים. כשאנחנו לומדים את המשוואות, אנחנו רואים תמונה אחת. כשאנחנו מודדים את המערכת, אנחנו מקבלים תמונה אחרת. פרדוקס זה ידוע גם כבעיית המדידה.
בעיית המדידה מובילה לתופעות מוזרות כמו חתול שרדינגר. החתול מתואר על ידי פונקציית גל, שהיא סופרפוזיציה לינארית של שני מצבים: החתול חי והחתול מת. כך שהחתול המסכן נמצא במצב סוריאליסטי של אנימציה מושעית, תקוע איפשהו בין להיות מת או חי. נדרש צופה כדי לגרום לקריסת פונקציית הגל של החתול ולהביא אותו לוודאות: או להיות מת או חי.
חלק מהמוחות הגדולים ביותר של המאה ה-20, כולל המתמטיקאי היהודי-הונגרי הגאון, ג’ון פון נוימן, חתן פרס נובל בפיזיקה, יוג’ין ויגנר, ופרופסור לפיזיקה בפרינסטון, המנוח ג’ון ארצ’יבלד וילר (ריצ’רד פיינמן היה תלמידו), כולם חשבו שרק תודעה אנושית יכולה לגרום לקריסת פונקציית הגל. זה הוביל את ג’ון וילר לטבוע את המונח, צופה משתתף, שמשמעותו היא שפעולת התצפית אינה פסיבית – הצופה משתתף ביצירת המציאות על ידי קריסת פונקציית הגל.
מנקודת מבט של ניתוח מבני, הגישה של התורה מקבילה לגישה הקוונטית-מכנית: חשוד, שעשוי להיות חף מפשע או אשם, כמו חתול שרדינגר, נמצא במצב של סופרפוזיציה לינארית של שני מצבים: אשם וחף מפשע. רק עד ראייה, כלומר צופה מודע, יכול לגרום לקריסת פונקציית הגל שלו ולהביא ודאות במקום אי-ודאות. זו הסיבה, לדעתי הצנועה, שהתורה דורשת עדות של עד ראייה כדי להרשיע חשוד – אנחנו זקוקים לעד ראייה, צופה משתתף, כדי לגרום לקריסת “פונקציית הגל” של הנאשם ולפתור את אי-הוודאות.
ב. מדוע עד ראייה אחד אינו מספיק?
אולי ראיתם סרטים עם הרגע של פרי מייסון, כאשר העד על דוכן העדים מצביע על החשוד היושב באולם בית המשפט וקורא, “הוא עשה את זה!” זה מקל על חבר המושבעים להגיע להכרעה מעבר לספק סביר.
ב-QM, נדרש רק צופה אחד כדי לגרום לקריסת פונקציית הגל. אם כך, בהתאם להיגיון שלנו, עד ראייה אחד צריך להספיק כדי להרשיע פושע. מדוע התורה דורשת יותר מעד אחד? מדוע עד ראייה אחד, לא משנה כמה מכובד (במילות התלמוד, אפילו אם העד הזה הוא משה רבנו עצמו), אינו מספיק?
ההסבר המובן מאליו הוא שעד אחד לא יכול להיחקר כראוי, עדותו לא יכולה להיות מושווית לעדותו של עד ראייה אחר. התורה לוקחת את העיקרון של “חף מפשע עד שהוכחה אשמתו” לרמה חדשה לגמרי. התורה בכוונה מקשה מאוד על הרשעת הנאשם, כמעט בלתי אפשרי. כל העונשים הנוראיים המפורטים בתורה, כמו סקילה, עריפת ראש וחנק – נועדו כהרתעה – “ושמעו ויראו ובערת הרע מקרבך”, הוא פזמון נפוץ בתורה. לכן, התורה דורשת לפחות שני עדים כדי שהשופטים יוכלו לחקור אותם ולהעמיד את עדותו של האחד מול השני כך שניתן יהיה למצוא אי-התאמה והעדות תיפסל בבית המשפט. אין לנו לדאוג שפושעים רבים יצאו לחופשי. בסופו של דבר, אלה שביצעו פשעים נוראיים לא יישארו ללא עונש, אבל העונש יבוא מ”ידי שמים”. זה מלמד אותנו לא להיות יהירים ולא לשחק את תפקיד האלוהים, אלא לסמוך עליו שיבצע צדק בעולם.
פילון שיבח את הדרישה שבית משפט לא יסתמך על עדות של עד יחיד כ”מצווה מצוינת”. פילון חשש שאדם עלול להיות מוטעה על ידי רושם ראשון כוזב. יתר על כן, מדוע שבית המשפט יקבל את דברי עד אחד כנגד דברי הנאשם? כאשר אין עדיפות לראיות, אין לקבל הכרעה, טען פילון.
אולי סיבה נוספת יכולה להיות ההבנה העמוקה שהידע האנושי אינו מושלם וכפוף לאי-ודאות. רק הקב”ה, שהוא כל-יודע, יש לו ידע מושלם כי הוא יודע הכל על ידי ידיעת עצמו. זוהי הצהרה של ענווה, להכיר בכך שאדם אחד לעולם לא יכול להשיג את הידע והוודאות המושלמים, שהם תחומיו של הקב”ה. זו אולי עוד סיבה לכך שהתורה דורשת יותר מעד אחד כדי להרשיע חשוד בפשע. גם אז, אנו מבינים שעדותם של שניים או יותר עדים, במקרה הטוב, היא קירוב לידע המושלם של הקב”ה. זו דרכנו להתמודד עם אי-הוודאות המובנית בידע האנושי. במילותיו של קרל פופר, פילוסוף מדע בולט במאה ה-20, אנחנו יכולים להיות בטוחים רק שתיאוריה שגויה; לעולם לא נוכל להיות בטוחים שהיא נכונה. התורה לימדה אותנו זאת הרבה לפני פופר.
אי-ודאות, חקירת שני עדים… מושגים אלה מעוררים דמיון מעורפל לעקרון אי-הוודאות של הייזנברג. על פי עקרון אי-הוודאות, שהוא הבסיס לפיזיקה קוונטית, לעולם לא נוכל להיות בטוחים בערכים של שני מאפיינים משלימים, לעולם לא נוכל למדוד תכונות כאלה בדרגת דיוק בלתי מוגבלת. קחו לדוגמה זוגות כאלה של תכונות משלימות כמו מיקום ותנע, או זמן ואנרגיה. על פי עקרון אי-הוודאות, מכפלת אי-הוודאויות במדידות של תכונות אלה חייבת תמיד להיות שווה או גדולה מקבוע פלאנק. אם, לדוגמה, ∆x היא אי-הוודאות במדידת המיקום של חלקיק ו-∆p היא אי-הוודאות במדידת התנע של חלקיק זה, אז
באופן דומה, אם ∆t היא אי-הוודאות במדידת הזמן ו-∆E היא אי-הוודאות במדידת האנרגיה, אז
הבה נתבונן כעת בעדותם של שני עדים. קל להבין שהם משלימים במובן הקוונטי-מכני – ככל שעדות אחת מדויקת יותר, כך השנייה חייבת להיות פחות מדויקת כדי לא לסתור את הראשונה. נניח, לדוגמה, שהעד הראשון מעיד שהפשע התרחש בבוקר. למרות שהעד השני אינו מודע לעדותו של העד הראשון – הם נחקרים בנפרד – קל לו גם לומר שהפשע בוצע בבוקר. אולם, אם העד הראשון אומר שהפשע בוצע ב-10:01 בבוקר והעד השני אומר שהוא בוצע ב-10:02, שתי העדויות אינן עקביות ונפסלות בבית המשפט. לכן, כדי לא לסתור את העד הראשון, העד השני צריך לומר שהפשע בוצע בשעות הבוקר אך אינו זוכר את השעה המדויקת. ככל שעדותו של העד הראשון מדויקת יותר, כך עדותו של העד השני צריכה להיות מעורפלת יותר כדי לא לסתור את הראשון. בדיוק כמו במכניקת הקוונטים, שבה מכפלת אי-הוודאויות במדידות של תכונות משלימות אינה יכולה להיות אפס, גם כאן, מכפלת אי-הוודאויות בעדויות של שני העדים אינה יכולה להיות אפס. השופטים משתמשים בזה כדי למצוא סתירות בעדויות העדים לפסול אותן ולזכות את הנאשם. מכיוון שזו המטרה, התורה מספקת מנגנון פשוט להשיג זאת, ובינתיים, מלמדת אותנו משהו על פיזיקה קוונטית.
III שניים או שלושה עדים
על פי התורה, לא ניתן להרשיע חשוד על פי עדות של עד אחד. “על פי שני עדים או שלושה עדים…” מדוע התורה אומרת “שני עדים, או שלושה עדים”? אם שני עדים מספיקים, בוודאי ששלושה גם יספיקו!
התלמוד (מכות, ה ע”ב) מסביר שאם העד השלישי סותר את שני העדים האחרים, העדות אינה קבילה. אף על פי שבהכרעת עניינים הלכתיים (שאלות של קיום מצוות) בית הדין הולך אחר הרוב, בעניינים פליליים, באופן מפתיע, אין זה המקרה. אפילו אם בקבוצה של 100 עדים, 99 מהם מאשרים את עדותם זה של זה, אך עד אחד סותר אותם, כל 100 העדים נפסלים ועדותם נזרקת מבית המשפט. כל העדים מטופלים כקבוצה אחת. קשה להבין זאת כיוון שזה נראה מנוגד לאינטואיציה.
התלמוד מסביר עוד שכל העדים המציעים את עדותם על פשע חייבים לצפות לא רק בפשע אלא גם למסור עדות זה על זה במהלך אותו פשע. במבט ראשון, זה נראה חסר היגיון – מה זה משנה אם העדים ראו זה את זה במהלך הפשע? כל עוד כולם ראו את הפשע ונתנו עדות זהה, זה היה צריך להספיק!
מסתבר שפרט זה בדין העדים הוא המפתח להבנה מדוע כל העדים מטופלים כקבוצה אחת. על ידי ראיית זה את זה, העדים מסתבכים זה בזה. בשפה של מכניקת הקוונטים, הם חולקים את אותו מצב, כלומר, הם מתוארים על ידי אותה פונקציית גל. כאשר מטפסי הרים מטפסים לפסגה כשהם קשורים זה לזה בחבל אחד, אם אחד נופל, הוא או היא יכולים להפיל את כל הקבוצה איתם. כך גם כאן, מכיוון שכל העדים מסובכים, עד אחד יכול לפסול את כל הקבוצה ללא קשר לגודלה. עדים בהלכה היהודית חייבים לא רק לראות את הפשע אלא גם לראות ולהיראות על ידי זה את זה. זה נותן משמעות חדשה לביטוי הישן – לראות ולהיראות.