וידבר אתם לאמר… שמעוני ופגעו־לי באפרון בן־צחר. ויתן־לי את־מערת המכפלה אשר־לו אשר בקצה שדהו… (בראשית כג:ח-ט)
מכפלה: בית שיש עליו עלייה. דבר אחר: על שם שנכפלה בזוגות (עירובין נג ע”א) (רש”י על בראשית כג:ט)
בפרשת חיי שרה, אברהם רכש מערת מכפלה כמקום קבורה אבותי. כמעט כל פרשני המקרא הקלאסיים מפרשים את מכפלה (כלומר, “כפולה”) כמערה עם שני חדרים. רש”י נוקט גישה שונה לחלוטין וקובע שהמערה הייתה ידועה בזכות בית דו־קומתי שנבנה מעליה. כך, המילה מכפלה מתייחסת לא למערה עצמה, אלא לבית שנבנה מעל המערה. מוזר עוד יותר הוא שרש”י מציע פרשנות חלופית הקובעת שהמילה “כפולה” עשויה להתייחס גם לזוגות האבות הקבורים שם—אדם וחוה, אברהם ושרה, יצחק ורבקה, ויעקב ולאה. מה הקשר בין שתי הפרשנויות השונות הללו?
יש תעלומה עמוקה בפיזיקה. למרות שהיא ממש על פני השטח בוהה בעינינו, לא תמצאו אזכור אליה באף ספר לימוד בפיזיקה; לא תשמעו אף פרופסור מזכיר אותה בהרצאה (אני כן עשיתי זאת, אבל מעולם לא שמעתי על מישהו אחר שדיבר על כך). אפילו לא צריך להיות בעל דוקטורט בפיזיקה כדי להבין זאת — כל תלמיד תיכון הלומד מכניקה ניוטונית אמור להיות מסוגל לתפוס זאת. הנה היא.
החוק השני של ניוטון קובע שלכל גוף,
a × m = F, או a = 1/m × F,
כאשר a הוא התאוצה של הגוף, m הוא המסה של הגוף, ו־ F הוא הכוח הכולל הפועל על הגוף. בעיקרו של דבר, החוק השני של ניוטון קובע שהתאוצה a של גוף עם המסה m פרופורציונלית לכוח F הפועל על הגוף (כאן, האותיות המודגשות מציינות וקטורים, כלומר כמויות שיש להן גם גודל וגם כיוון; מהירות, תאוצה וכוח הם וקטורים, בעוד שמסה היא סקלר—כמות ללא כיוון).
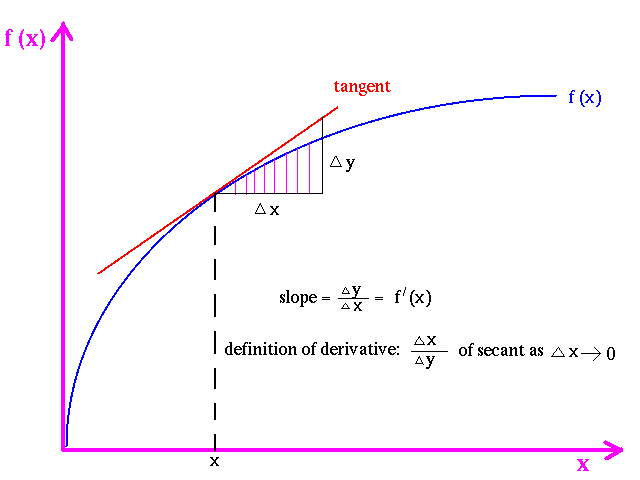
איפה התעלומה, תוכלו לשאול? לשם כך, אנחנו זקוקים לקצת מתמטיקה. המהירות של עצם היא הנגזרת הראשונה של מיקום העצם במרחב לאורך זמן: v = dx/dt.
במילים פשוטות, נגזרת מודדת את הרגישות לשינוי של ערך הפונקציה (ערך הפלט) ביחס לשינוי בארגומנט שלה (ערך הקלט). הנגזרת של פונקציה היא השיפוע של הקו המשיק לגרף הפונקציה באותה נקודה.
בית הבנוי על פני השטח של כדור הארץ הוא גם משיק לפני השטח:

התאוצה היא מהירות של המהירות, כלומר, נגזרת של המהירות לאורך זמן: a = dv/dt.
זה הופך אותה לנגזרת השנייה (נגזרת של הנגזרת) של המיקום לאורך זמן: a = d2x/dt2.
הנגזרת של פונקציה היא המהירות שבה הפונקציה הזו משתנה עם השינוי של הארגומנט. הנגזרת עצמה היא פונקציה—מבנה מתמטי שאנו בונים על גבי הפונקציה המקורית. מכיוון שהיא פונקציה בפני עצמה, אנו יכולים לקחת נגזרת של אותה פונקציה—הנגזרת השנייה של הפונקציה המקורית ולבנות עוד מבנה “על גבי” הפונקציה המקורית, ה”קומה העליונה” מעליה. כך, במטפורה, ניתן לחשוב על הנגזרת השנייה כמבנה דו־קומתי הנבנה על גבי הפונקציה המקורית.
הנגזרת השנייה צצה בכל מקום בפיזיקה ונראה שהיא מייצגת חוק יסודי של דינמיקה.

במהלך נאום קבלת פרס נובל שלו, הפיזיקאי יוג’ין ויגנר אמר שתפקיד המדע הוא להפריד דפוסים מרעש. זו הייתה אחת ההצהרות החדות ביותר ששמעתי על טבע המדע. זה מה שניוטון עשה עם החוק השני שלו.
בואו נדמיין שאנחנו חיים לפני ניוטון, ואנחנו מנסים לחקור את התנועה של עצם. היינו צופים בתנועה כזו פעמים רבות, מציינים את ההתאמה בין מיקום העצם לזמן שבו נמדד המיקום הזה. בסוף ניסוי ארוך, היינו צוברים כמות גדולה של נתונים—נקודות על הגרף המתווה את מיקום העצם במהלך הזמן. היינו יכולים לדמיין שחלק מהנתונים הללו הוא אקראי (כלומר, רעש), וחלק מייצג איזה דפוס—החוק הפיזיקלי שעדיין לא ידוע. כל התהליכים הדינמיים בפיזיקה מתוארים על ידי משוואות דיפרנציאליות (כמו החוק השני של ניוטון). אם היינו מניחים שהדפוס הלא ידוע שלנו מתואר על ידי משוואה דיפרנציאלית מסדר ראשון (הנגזרת הראשונה), כדי לפתור אותה, היינו צריכים לבצע אינטגרציה, מכיוון שהאינטגרל הוא ההפך מהנגזרת. עם זאת, הנגזרת של קבוע היא תמיד אפס, מה שאומר שכאשר אנו הופכים את פעולת הגזירה על ידי לקיחת אינטגרל, אנו יכולים לדעת את התשובה רק עד כדי קבוע. מה שזה אומר הוא שאם הדפוס שלנו מתואר על ידי משוואה דיפרנציאלית מסדר ראשון (הנגזרת הראשונה), תהיה לנו שכבה של רעש אקראי המיוצגת על ידי הקבועים הצצים במהלך האינטגרציה. כדי להיפטר מהם, אנחנו צריכים לבחור את התנאים ההתחלתיים. במקרה של עצם נע, היינו צריכים לדעת את המיקום ההתחלתי של העצם.
אם, עם זאת, הדפוס שלנו מתואר על ידי המשוואה הדיפרנציאלית מסדר שני (הנגזרת השנייה), כדי לפתור אותה, היינו צריכים לבצע אינטגרציה פעמיים, מה שמייצר שתי קבוצות של קבועים ולכן שתי שכבות של רעש אקראי. כדי להיפטר מהרעש הזה, היינו צריכים לדעת שתי קבוצות של תנאים התחלתיים. במקרה של עצם נע, היינו צריכים לדעת את המיקום ההתחלתי והמהירות ההתחלתית שלו.
הגאונות של ניוטון הייתה לנחש שהחוק הבסיסי של המכניקה (וכפי שהתברר מאוחר יותר, של דינמיקה בכלל) הוא המשוואה הדיפרנציאלית מסדר שני (הנגזרת השנייה). זו הסיבה שבמכניקה, כדי לחזות מיקום עתידי של עצם בנקודת זמן מסוימת, אנחנו צריכים לדעת את המיקום ההתחלתי והמהירות שלו—אנחנו צריכים זוג תנאים התחלתיים. במתמטיקה, התנאים ההתחלתיים הם אבותיהם של הערך העתידי של הפונקציה—”אבות”, אם כן.
כעת, כל חלקי החידה מתחברים יחד: המבנה עם הקומה השנייה על גבי המערה בפרשנות הראשונה של רש”י הוא מטפורה של הנגזרת השנייה—המבנה דו־הקומתי שאנו בונים על גבי הפונקציה המקורית. הזוגות הקבורים במערה מתייחסים לזוג תנאים התחלתיים הדרושים לפתרון המשוואה עם הנגזרת השנייה.
בעוד שהנגזרות השניות נפוצות בכל מקום בפיזיקה, תמיד חשבתי שזה עיקרון אוניברסלי. מסיבה כלשהי, בכל פעם שאנחנו רוצים לחקור את האבולוציה של מערכת דינמית בזמן, יתברר שהנגזרת השנייה היא זו שמייצגת את הדפוס עם שתי שכבות של רעש אקראי הקשורות אליה.
זו הסיבה שניסיון להתאים עקומה להתנהגות השוק בעבר כדי לחזות מחירי מניות עתידיים הוא משימה של שוטים—הייתם מערבבים יחד דפוסים עם רעש. ייתכן שתוכלו לחזות את מחיר המניה העתידי (או המחיר של כל סחורה או מכשיר פיננסי) על ידי התחשבות בנגזרת השנייה של המחיר לאורך זמן. אם אתם רוצים להתעשר, זה עתה אמרתי לכם איך.
אפילו ברפואה, כאשר אנחנו עושים בדיקות, זה לא כל כך הערך הנוכחי של הבדיקה שחשוב, אלא איך הוא “מאיץ” בזמן, כלומר, הנגזרת השנייה. אכן, במחקר אחד על הרלוונטיות של PSA כסמן חיזוי לסרטן הערמונית, המחקר הראה שזו הייתה הנגזרת השנייה—התאוצה בעלייה של PSA—שהייתה בעלת הערך החיזוי הגדול ביותר. אכן, הנגזרת השנייה שולטת! זה לא אומר שבדיקות סטטיות המראות תמונת מצב בזמן אינן שימושיות. אבל אם נוכל לחזור על בדיקה לעתים קרובות ולחשב את הנגזרת השנייה, זה ייתן לנו ערך אבחנתי הרבה יותר גדול.
אולי, רש”י רמז לנו על הסוד הזה על ידי הסבר משמעות המילה מכפלה כמבנה דו־קומתי על גבי המערה.