דפוסים פרקטליים בתורה

בפרשת אמור (ויקרא כא:א-כד:כג), אנו מצווים להימנע ממלאכה בכל יום שביעי בשבת. פרשת השבוע הבאה, בהר, ממשיכה נושא זה ומורה לנו להימנע מעבודה חקלאית בכל שנה שביעית, שמיטה. והתורה לא עוצרת שם. היא מורה לנו לספור שבע שמיטות ואז לשמור על היובל, יובל.

האם אתם מבחינים בדפוס? כל שבעה ימים, כל שבע שנים, כל שבע שמיטות… יתר על כן, המדרש קובע שהעולם יתקיים שבעת אלפים שנה כאשר האלף השביעי יהיה אלף שנות מלכות משיח—יום שכולו שבת—שבת ארוכה אחת. חכם מהמאה השנייה, רבי חוניה בן הקנה, מפרש מדרש זה כמשמעותו שהעולם יימשך שבע שמיטות קוסמיות, כלומר 49 אלף שנים (אשר, לפי המקובל הבולט מהמאה ה-13-14 רבי יצחק דמן עכו, אינו מדבר על שנים ארציות אלא על שנים שמימיות השוות לכ-15 מיליארד שנים—לא רחוק מהאומדן הנוכחי של גיל היקום הקוסמולוגי של 13.8 מיליארד שנים, אך זה נושא אחר.)

המשותף כאן הוא דמיון עצמי בקני מידה שונים—המספר שבע משחק תפקיד של תקופה בספירלה רב-ממדית עם תקופות מרובות: שבעה ימים, שבע שנים, שבע שמיטות (ליתר דיוק, שבע שמיטות ועוד אחת, שכן היובל הוא בשנה החמישים), שבעה אלפי שנים, שבע שמיטות קוסמיות… במתמטיקה, דפוסים כאלה נקראים פרקטלים. פרקטל, לפי הגדרה, הוא דפוס החוזר על עצמו בכל קנה מידה. תכונה זו נקראת דמיון עצמי.

גיאומטריה פרקטלית היא תחום מרתק וחדש יחסית במתמטיקה. כמה מהדוגמאות הפשוטות ביותר של קבוצות פרקטליות הן:

קבוצת קנטור. כדי לבנות קבוצת קנטור, אנו מציירים תחילה קו. אנו מחלקים קו זה לשלושה מקטעים ומסירים את המקטע האמצעי. אנו ממשיכים בתהליך זה עד אין סוף. הנה קבוצת קנטור לשבעה איטרציות:

פתית השלג של קוך. את פתית השלג של קוך ניתן לבנות על ידי התחלה במשולש שווה צלעות, ואז שינוי רקורסיבי של כל קטע קו כדלהלן:

1. אנו מחלקים את קטע הקו לשלושה מקטעים באורך שווה.
2. אז אנו מציירים משולש שווה צלעות שיש לו את המקטע האמצעי משלב 1 כבסיס שלו ופונה החוצה.
3. לבסוף, אנו מסירים את קטע הקו שהוא בסיס המשולש משלב 2.

אנו חוזרים על תהליך זה עד אין סוף. אי אפשר שלא להבחין שהאיטרציה השנייה של האלגוריתם מייצרת את מגן דוד, מגן דוד. תכונה מדהימה של פתית השלג של קוך היא שיש לו שטח סופי המוקף בקו אינסופי באורכו.

משולש סירפינסקי. פרקטל זה הוא משולש שווה צלעות, המחולק באופן רקורסיבי למשולשים שווי צלעות קטנים יותר.

הוא נבנה על ידי הסרת תת-קבוצות משולשיות:

1. אנו מתחילים עם משולש שווה צלעות.
2. אנו מחלקים אותו לארבעה משולשים שווי צלעות קטנים יותר ומסירים את המרכזי.
3. אז אנו חוזרים על שלב 2 עם כל אחד מהמשולשים הקטנים הנותרים, וכן הלאה.

שטיח סירפינסקי:

שטיח סירפינסקי דומה מאוד למשולש סירפינסקי כאשר במקום משולשים, אנו משתמשים בריבועים:

חופת פרקטל. לחופת פרקטל יש את שלוש התכונות הבאות:

1. הזווית בין כל שני קטעי קו שכנים זהה לאורך כל הפרקטל.
2. היחס בין אורכי כל שני קטעי קו עוקבים הוא קבוע.
3. נקודות בקצה של קטעי הקו הקטנים ביותר מחוברות ביניהן.

המכנה המשותף של כל התמונות הללו הוא דמיון עצמי בכל קנה מידה. חלק מהפרקטלים הם יפים באופן היפנוטי. הביטו למשל בפרקטל קבוצת ז’וליה זה:

צורות פרקטליות קיימות לא רק במתמטיקה, אלא הן גם סביבנו בכל מקום. המתמטיקאי היהודי בנואה מנדלברוט שם לב שחלק גדול מהטבע יש לו צורה פרקטלית—בין אם זה עלה מייפל, כרובית, הרים, קו חוף, ריאות, או כלי דם—לכולם יש תכונה משותפת אחת, דמיון עצמי בקני מידה שונים. (לפני מספר שנים, שיערתי שהמרחב-זמן שלנו, בעוד שהוא חלק בקנה מידה גדול, חייב להיות פרקטלי בקנה מידה מיקרוסקופי. אם זה נכון, ה’גסות’ הפרקטלית הזו בקנה מידה קטן עשויה להיות מסוגלת לגשר על הפער בין תורת היחסות הכללית לתורת השדה הקוונטי.) פרקטלים נמצאים בכל מקום בטבע. מדוע זה כך?

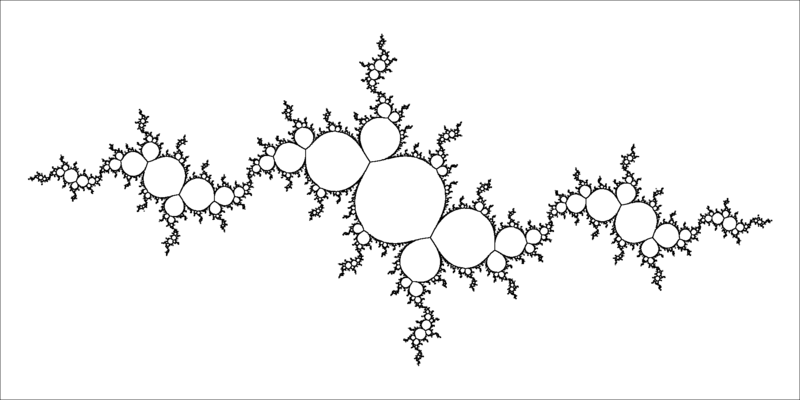
נראה לי שהסיבה לכך טמונה במבנה הספירות בעולם התיקון. ספירות—האצלות אלוהיות שהן ‘אבני הבניין’ של הבריאה—הן המסגרת המושגית הבסיסית של כל הבריאה. בעוד שבעולם התוהו הספירות מנותקות, מה שהוביל לשבירת הכלים, בעולם התיקון הן כלולות זו בזו, כלומר, כל ספירה כוללת את כל עשר הספירות. כך, חכמה כוללת את כל עשר הספירות: חכמה של חכמה, בינה של חכמה, דעת של חכמה, חסד של חכמה, גבורה של חכמה, תפארת של חכמה, נצח של חכמה, הוד של חכמה, יסוד של חכמה ומלכות של חכמה. עשר ספירות מתפצלות למאה צירופים. אנו נמצאים כעת בימי ספירת העומר, כאשר בכל יום אנו מתקנים צירוף מסוים של שבע מידות (שבע ספירות תחתונות) סופרים חסד של חסד, גבורה של חסד, וכו’—49 צירופים בסך הכל. כל אחד ממאה הצירופים, בתורו, כולל גם כן את כל עשר הספירות מה שמוביל להתפצלות נוספת של עץ הספירות, עד אין סוף. זהו מבנה פרקטלי מושלם. אין פלא שהעולם הפיזי, המשקף את מקורו הרוחני, מציג דפוסים פרקטליים דומים. בעוד שהטבע מספק דוגמאות רבות לדפוסים פרקטליים במרחב, התורה מראה לנו דפוס פרקטלי ייחודי בזמן ובתחום הרוחני.

דפוס פרקטלי נוסף הייחודי לתורה נמצא באחד מכלי הפרשנות המקראית—גימטריה. בעברית, המספרים נכתבים באמצעות אותיות האלף בית: 1 הוא אלף, 2 הוא בית, וכו’. לכן, לכל אות עברית יש ערך מספרי, גימטריה. הדרך הפשוטה ביותר לחשב את הגימטריה של מילה עברית היא לחבר את הערכים המספריים של כל האותיות המאייתות את המילה. לדוגמה, המילה אחד מאויתת אלף-חית-דלת. הערכים המספריים של אותיות אלה הם: אלף=1, חית=8 ודלת=4. לכן, הגימטריה של אחד היא 1+8+4=13. אולם, לכל אות יש את שמה ולכן את הגימטריה שלה: אלף מאויתת אלף-למד-פה, אז הגימטריה שלה היא 1+30+80=111. חית מאויתת חית-יוד-תו, אז הגימטריה שלה היא 8+10+400=418. דלת מאויתת דלת-למד-תו, אז הגימטריה שלה היא 4+30+400=434. הרחבת כל אות של המילה אחד עם האיות של כל אות נותנת אלף-למד-פה-חית-יוד-תו-דלת-למד-תו, אז הגימטריה המורחבת של אחד היא 111+418+434=963. גימטריה כזו נקראת מילוי (מלא). כל אות באיות המורחב, מילוי, יכולה בתורה להיות מאויתת שוב, עד אין סוף. שוב, יש לנו דפוס פרקטלי.

כל הפרשנות התורנית היא פרקטלית באופייה. ישנן חמש רמות של פרשנות תורה הנקראות בראשי התיבות שלהן, פרד”ס (גן):

1. פשט (משמעות מילולית)
2. רמז (רמז)
3. דרש (דרשנות)
4. סוד (‘סוד’ – קבלה)
5. סוד שבסוד (‘סוד הסודות’—חסידות)

בתורן, לכל אחת מרמות אלה יש גם חמש רמות, כך שיש לנו פשט של פשט, רמז של פשט וכו’—מבנה פרקטלי.

בקנה מידה רחב יותר, ה’ ברא איש ואישה בצלמו. הוא ציווה עליהם להתרבות. זה הניע את עץ האנושות המתרחב והמסתעף ללא הרף. כפי שבנואה מנדלברוט הסביר, פרקטל הוא ‘צורה בעלת התכונה שכל חלק קטן ממנה יכול להיראות כעותק מוקטן של השלם’. כשמסתכלים על אדם, לא משנה כמה קטן, לעולם אל נשכח שזהו עותק מיניאטורי של ה’. בואו נגלה קצת כבוד!