Зрелище Вселенной становится тем грандиознее, тем прекраснее, тем достойнее своего Автора, когда знаешь, что небольшого числа законов, мудро установленных, достаточно для всех движений.
Пьер Луи Мопертюи (1744)
Среди более или менее общих законов, открытие которых характеризует развитие физической науки в течение последнего столетия, принцип наименьшего действия в настоящее время, безусловно, является одним из тех, которые по своей форме и всеохватности, можно сказать, наиболее близко подошли к идеальной цели теоретического исследования. Его значение, при правильном понимании, распространяется не только на механические процессы, но и на тепловые и электродинамические задачи. Во всех отраслях науки, к которым он применяется, он дает не только объяснение определенных характеристик наблюдаемых в настоящее время явлений, но и предоставляет правила, с помощью которых их изменения во времени и пространстве могут быть полностью определены. Он дает ответы на все вопросы, касающиеся их, при условии, что известны необходимые константы и соответствующим образом выбраны основные внешние условия.
Макс Планк (1909)
Содержание
II. Введение в принцип наименьшего действия
III. История <— Вы здесь
(c) Принцип наименьшего действия
VII. V. Духовный источник принципа наименьшего действия
Это третья часть серии о принципе наименьшего действия. В первой части, «Принцип наименьшего действия I», мы познакомились с телеологией. Мы узнали, что телеология — это причина или объяснение чего-либо, что служит функцией его цели, в отличие от чего-либо, что служит функцией его причины. Считается, что у него есть цель, задача или конец, к которому они стремятся. Конечная цель называется конечной причиной (causa finalis). Мы также узнали, что иудаизм, несомненно, телеологичен в своей основе и что еврейская вера основана на вере в целенаправленного Б‑га, который создал целенаправленный мир. Во второй части мы познакомились с принципом наименьшего действия. Мы узнали, что принцип наименьшего действия является формальным представлением таких простых идей, как эффективность и оптимизация. Природа стремится подражать своему Создателю как можно лучше. Следовательно, эффективность природы является проявлением совершенства бесконечного Творца в конечных пределах физического мира. В этой (третьей) части мы собираемся рассмотреть историю развития принципа наименьшего действия, что углубит наше понимание этого кардинального принципа науки.
III. История
Принцип наименьшего действия — это принцип, который играет фундаментальную роль в формулировке классической механики (как лагранжевой, так и гамильтоновой механики), релятивистской механики (как специальной, так и общей теории относительности), электродинамики, механики жидкости, квантовой механики, физики элементарных частиц, квантовой теории поля и теории струн. Он также используется в биологии, экономике и других областях за пределами физики. Его историческое развитие тесно переплетено с прогрессом физики и пониманием естественного мира. Краткий обзор его истории может помочь нам развить более глубокое интуитивное понимание этого принципа.
1. Античность

Рисунок 3. Евклид работы Юсепе де Риберы, ок. 1630–1635 гг. (Википедия, общественное достояние)
Самые ранние зерна этой идеи можно найти в Древней Греции. Евклид[1] написал в своей Катоптрике[2], что для пути света, отражающегося от зеркала, угол падения равен углу отражения,[3] что подразумевает, что луч света движется по кратчайшему пути — прямой линии.[4]
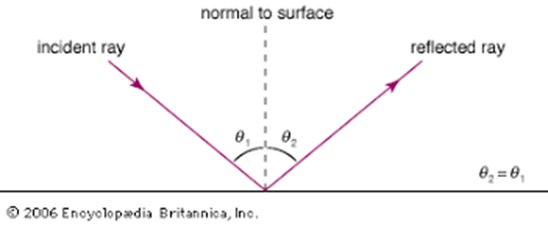
Герон Александрийский[5] в I веке нашей эры явно описал «закон отражения», используя концепцию «кратчайшего пути».[6] Это ранний намек на вариационные принципы в физике.

Рисунок 4. Немецкое изображение Герона Александрийского XVII века (Википедия, общественное достояние).
С теологической точки зрения, выбор правильного пути — dereḥ ha-yashar («прямой путь») — является религиозным императивом. Например, мы находим в Притчах:
Во всех путях твоих познавай Его, и Он направит (yasher) стези твои.
Притчи 3:6
Мы также находим этот императив в Псалмах:
Укажи мне, Господи, путь Твой, и направь меня на стезю прямую…
Псалмы 27:11
Пророчествуя о возвращении изгнанников во время окончательного искупления, Иеремия пишет:
Я поведу их к рекам водным дорогою ровною, на которой не споткнутся…
Иеремия 31:9
Лурианская Каббала учит, что после изначальных сокращений (Tzimtzum) — первоначального сокрытия божественного света Ohr Ain Sof — создавая пустое пространство (halal) для мира, Б‑г послал луч божественного света в пустое пространство. Этот луч света называется в Каббале кав ([прямая] линия). Стоит ли удивляться, что мир, созданный этой прямой линией кав, ведет себя аналогичным образом, выбирая прямой свет в качестве предпочтительной траектории движения?
2. Ренессанс
(a) Принцип Ферма

Рисунок 5. Портрет Пьера де Ферма неизвестного автора, 17 век (общественное достояние, Википедия)
Принцип наименьшего расстояния хорошо работает в частном случае, когда свет проходит через одну среду. Однако, когда свет проходит через две или более среды, такие как воздух и вода, он больше не движется по прямой линии — принцип наименьшего расстояния больше не работает в этом общем случае. В 1662 году французский математик Пьер де Ферма предложил «Принцип наименьшего времени» для распространения света, ныне известный в оптике как принцип Ферма. Он предположил, что свет проходит между двумя точками по пути, который требует наименьшего времени. Ему предшествовал в этом Готфрид Лейбниц.[7] Чтобы рассчитать путь света, распространяющегося через две среды, необходимо рассчитать время прохождения света в каждой среде отдельно (потому что свет движется с разной скоростью в разных средах), а затем минимизировать общее время, что даст угол преломления. Принцип наименьшего времени обобщает принцип наименьшего расстояния.

Рисунок 6. Готфрид Вильгельм Лейбниц, Кристоф Бернхард Франке, 1695 г. (Википедия, общественное достояние)
Чтобы развить интуитивное понимание принципа Ферма, давайте предположим, что вы любите ездить на велосипеде на работу и стремитесь добраться до своего офиса в кратчайшее время. Есть две дороги до вашего офиса — одна прямая грунтовая дорога, пересекающая травянистые лужайки и участки грязи, а другая — асфальтированная дорога, которая длиннее, но не имеет препятствий. Следуя принципу Герона о прямой дороге, вы бы выбрали внедорожную прямую дорогу и прибыли в офис с опозданием. Следуя по асфальтированной, хотя и более длинной дороге, вы быстрее доберетесь до офиса.
Другой, и, возможно, лучший пример привел Ричард Фейнман в своих лекциях. Скажем, спасатель, наблюдающий за пловцами на пляже, замечает, что кто-то тонет в океане. Он не собирается сразу прыгать в океан, а сначала побежит по пляжу, прежде чем войти в воду, потому что знает, что бегать по сухой поверхности быстрее, чем плавать в воде. Цель состоит в том, чтобы добраться до тонущего человека как можно быстрее — то есть минимизировать общее время. [8]
Выбор априори пути, который занимает минимальное время, имеет сильные телеологические оттенки. Ричард Фейнман подчеркнул это в своих знаменитых лекциях:
Идею причинности, что она идет от одной точки к другой и так далее, легко понять. Но принцип наименьшего времени — это совершенно другой философский принцип о том, как работает природа. Вместо того чтобы говорить, что это причинная вещь, что когда мы делаем одно, происходит что-то еще и так далее, он говорит следующее: мы создаем ситуацию, и свет решает, какое время самое короткое или экстремальное, и выбирает этот путь. Но что он делает, как он это узнает? Он чувствует близлежащие пути и сравнивает их друг с другом?[9]
Талмуд рассказывает историю о раввине Йеошуа, встретившем молодого мальчика на перекрестке. Раввин Йеошуа спросил мальчика, какая дорога ведет в город, и мальчик рассказал ему о двух дорогах — короткой, но длинной дороге и длинной, но короткой дороге. Раввин Йеошуа сначала пошел короткой, но длинной дорогой, которая была короче по расстоянию, но имела препятствия, продлевающие путешествие. Затем он понял слова мальчика. Есть более длинные пути, которые являются самыми быстрыми.[10] Раввин Шнеур Залман из Ляди выбрал это выражение — более длинный, но более короткий путь — в качестве эпиграфа к своей книге Тания.[11]
С точки зрения еврейского закона, Галахи, принцип наименьшего времени представляется предпочтительнее принципа наименьшего расстояния. Талмуд обсуждает ситуацию, когда священник (коэн) приобретает телесную нечистоту (тума) находясь в Храме (Бет ХаМикдаш).[12] Священнику не разрешается находиться в Храме в состоянии тума (ритуальной нечистоты). Должен ли он искать кратчайший или самый быстрый путь, чтобы покинуть священную территорию? Например, он может увидеть двое ворот, ведущих наружу, одни ближе к нему, а другие дальше. Он видит толпы людей, входящих на территорию Храма через ближайшие ворота, и понимает, что если он побежит к ближайшим воротам, его значительно замедлят толпы, идущие в противоположном направлении — он будет бежать против течения. Дальние ворота не загромождены, между ним и этими воротами нет толп. Очевидно, что, пытаясь минимизировать время своего недопустимого пребывания на пустой территории, священник, скорее всего, побежит к дальним воротам, потому что добраться до них займет меньше времени.
С точки зрения Каббалы, кажется уместным обобщить принцип кратчайшего расстояния с принципом Ферма. В духовной иерархии Каббалы время появляется «раньше» пространства. В мире Ацилут (высшем духовном мире) шесть мидот (нижние сефирот) — Ḥesed, Гвура, Тиферет, Нетцах, Ход и Йесод — составляют Седер ХаЗеманим («Порядок времен») — предшественник времени. [13] Пространство, которое появляется ниже на сефиротическом дереве в Малḥут Ацилут, наследует ту же структуру, где шесть мидот образуют шесть направлений (четыре направления компаса плюс вверх и вниз) в нашем трехмерном пространстве. Кроме того, в метафизике хасидской философии Хабада пространство отождествляется с настоящим, «зажатым» между прошлым и будущим.[14] Пространство, в некотором смысле, берет свое начало во времени. Действительно, время определяется как изменение, а пространство — как отсутствие изменения (стабильность, постоянство). Однако именно изменение является первичным, а не постоянство. Творение следует ритму ратцо в’шов (бег и возвращение).[15] Следовательно, постоянство является неестественным состоянием как для духовного, так и для физического мира. Отсюда следует, что время первично, а пространство вторично. Если принцип кратчайшего расстояния ограничен одной средой, то при рассмотрении более общего многосредового случая вполне естественно взглянуть на более высокую реальность, чем пространство, то есть на время, чтобы найти обобщение этого принципа. Таким образом, замена кратчайшего расстояния кратчайшим временем может отражать каббалистическое представление о том, что в своем духовном источнике время является более высокой концепцией, чем пространство, и, в некотором роде, охватывает пространство.
(b) Вариационное исчисление
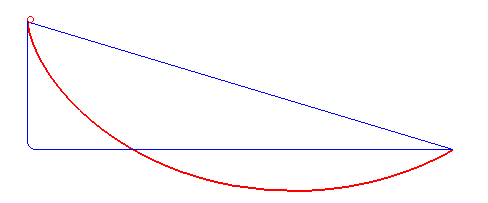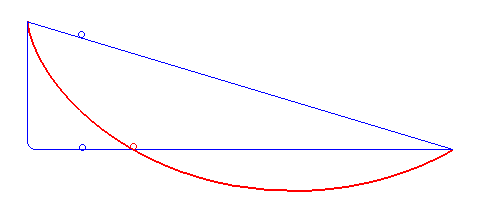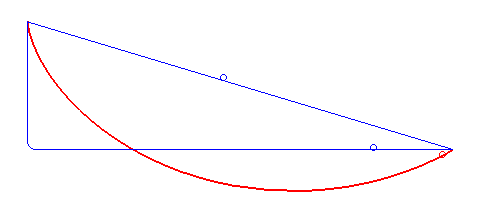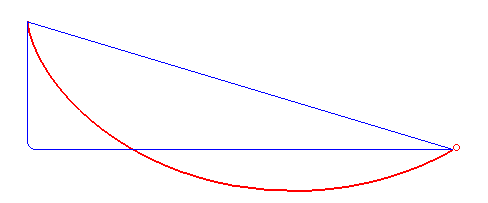
Рисунок 7. Кривая самого быстрого спуска — это не прямая или ломаная линия (синяя), а циклоида (красная). Автор: Роберт Ферреоль (общественное достояние, Wikimedia)

Рисунок 8. Иоганн Бернулли работы Иоганна Рудольфа Хубера, ок. 1740 г. (общественное достояние, Wikimedia)
В 1696 году Иоганн Бернулли[16] поставил задачу о брахистохроне[17]: «Какова форма кривой, по которой бусина под действием только силы тяжести будет скользить (без трения) из одной точки в другую за наименьшее время?» Решение этой проблемы, предложенное Иоганном и его братом и сотрудником Яковом Бернулли, а также Исааком Ньютоном и другими, использовало вариационный принцип. Они помогли развить вариационное исчисление как математическую дисциплину. [18]
(c) Принцип наименьшего действия
В XVIII веке, около 1746 года, французский математик и физик Пьер-Луи Моро де Мопертюи предложил принцип наименьшего действия, предполагая, что природа действует таким образом, чтобы минимизировать некоторую величину, связанную с действием. Как он знаменито сказал: «Природа бережлива во всех своих действиях». Хотя формулировка Мопертюи не была полностью общей или абсолютно верной, она ввела понятие, что такие вариационные принципы могут описывать природу.

Рисунок 9. Пьер Луи Моро де Мопертюи, гравюра Ж. Долле, 1741 год, по Р. Лерак-Турньера, 1737 год (общественное достояние, Викимедиа)
Как упоминалось ранее, математически вариационный принцип выражается в простой формуле:
δS = 0
Подобно тому, как в обычном исчислении исчезающая производная означает экстремальное (минимальное или максимальное) значение функции, в вариационном исчислении исчезающая вариация означает экстремальное (минимальное или максимальное) значение функционала S (действия).
Интересно отметить, что Мопертюи не ставил перед собой цель разработать новый подход к физике. Он разработал свой принцип наименьшего действия, который опубликовал в 1750 году в тонкой брошюре под названием «Опыт космологии», с единственной целью доказать существование Б‑га. Он писал:
Законы движения и покоя, выведенные из этого принципа, в точности совпадают с теми, что наблюдаются в природе, поэтому мы можем восхищаться его применением ко всем явлениям. Движение животных, вегетативный рост растений… — это лишь его следствия; и зрелище вселенной становится тем более величественным, тем более прекрасным, тем более достойным своего Автора, когда знаешь, что небольшого числа законов, мудро установленных, достаточно для всех движений. [19]
Эта цитата показывает, как Мопертюи связывал свой принцип с идеей великого, божественно упорядоченного космоса. Он верил, что несколько простых, элегантно установленных законов управляют всеми движениями и явлениями во вселенной, и это было свидетельством мудрости Творца. Хотя его брошюра была встречена насмешками со стороны современных интеллектуалов, в конце концов, его математика заложила основу современной физики. Я считаю, что, как Мопертюи был прав в своей математике, он прав и в приписывании единства и элегантности замысла мудрости Творца.
Предположение, что природа действует таким образом, чтобы минимизировать некоторую величину, является телеологическим по определению — физическое поведение объясняется постулированием цели, конечной причины.

Рисунок 10. Леонард Эйлер Якоба Эмануэля Хандманна (общественное достояние, Викимедиа)
Леонард Эйлер,[20] один из самых плодовитых математиков в истории, внес большой вклад в развитие принципа наименьшего действия, сформулировав уравнения движения, известные теперь как уравнения Эйлера-Лагранжа. Он часто переплетал свои научные труды с теологическими размышлениями. Он верил в рациональный порядок вселенной и видел руку Б‑га в ее замысле.
В своих «Письмах к немецкой принцессе» Эйлер пишет на различные темы, затрагивая гармонию вселенной и ее связь с Творцом. Он писал:
Поскольку ткань вселенной совершенна и является творением мудрейшего Творца, во вселенной не происходит ничего, в чем не проявлялось бы какое-либо правило максимума или минимума.[21]
Этот отрывок отражает веру Эйлера в божественно упорядоченную вселенную, где мудрость Б‑га очевидна в совершенстве и эффективности ее замысла.
Жозеф-Луи Лагранж[22] также внес основополагающий вклад в вариационное исчисление и дальнейшее развитие понятия наименьшего действия в механике, что привело к лагранжевой формулировке классической механики.

Рисунок 11. Жозеф-Луи Лагранж (общественное достояние, Викимедиа)
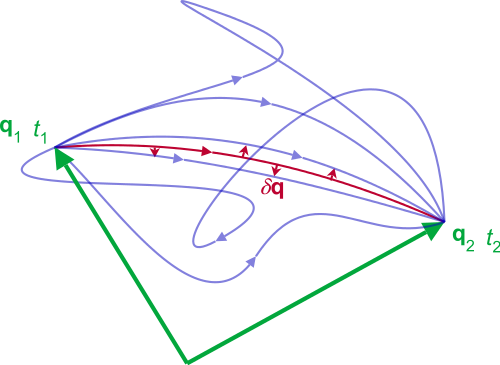
Когда мы ищем путь частицы, по мере ее эволюции от начального момента T1 до конечного момента T2, вполне естественно использовать вариационное исчисление. Еврейское слово shanah («год») обычно используется как эвфемизм для времени.[23] Shanah родственно слову shinui («изменение» или «вариация»). Таким образом, мы варьируем действие, чтобы определить эволюцию во времени.
Другой способ взглянуть на это предлагает Маймонид, который утверждает в своем главном труде Mishneh Torah, что правильный путь — это средний путь (dereḥ ha-nimtzoi):
Правильный путь — это середина в каждой группе предрасположенностей, общих для человечества; а именно, та предрасположенность, которая равноудалена от двух крайностей в своем классе, не будучи ближе к одной, чем к другой.[24]
Как нам достичь этого среднего пути? В каббале древо сфирот имеет три колонны — среднюю колонну (Кетер, Тиферет, Йесод, Малḥут), правую колонну (Ḥokhmah, Ḥesed, Netzaḥ), и левую колонну (Binah, Gevurah, Hod). В идеале нам настоятельно рекомендуется следовать средним путем (или колонной). В действительности, однако, мы пытаемся найти этот средний путь, отклоняясь немного вправо, каждый раз исправляя себя, чтобы вернуться к середине, но промахиваясь и отклоняясь немного влево, снова исправляя себя, чтобы вернуться к середине, и так далее. Это колебание между противоположными крайностями в попытке достичь среднего пути является духовным эквивалентом вариационного принципа, посредством которого мы варьируем траекторию (путь частицы), чтобы найти самый прямой (или самый быстрый) путь.
Это духовная версия вариационного принципа.
Теологическая параллель с принципом наименьшего действия основана на подражании Б-гу. Есть много способов прожить свою жизнь. Какой путь нам следует выбрать? Тора учит нас, что правильный путь — это подражать Б‑гу во всех наших путях.[25] Как написано:
Будьте святы, ибо Я, Господь Бог ваш, свят.
Левит 19:2
Мы должны быть справедливы, потому что Б‑г справедлив; мы должны быть добры, потому что Б‑г добр и т. д. В концептуальном пространстве, где расстояние измеряется степенью сходства, повеление подражать Б‑гу может быть математически выражено как минимизация расстояния, которое отделяет нас от Б‑га. Чем больше мы действуем как Б-г, тем ближе мы к Б‑гу. Однако не только люди должны подражать Б‑гу; вся природа должна! Действительно, мы находим в Иове:
…И я во плоти моей узрю Бога.
Иов 19:26
«Плоть» в этом стихе — это эвфемизм для материи или природы. Мы можем видеть Б‑га в природе, в материальном мире, потому что он тоже подражает Б‑гу. Мидраш говорит, что Богу было так же легко создать мир, как нам произнести букву Heh, пятую букву alefbet (еврейского алфавита), которая произносится просто выдыханием. Мудрецы говорят нам, что творение было для Бога легким. Bereshit Rabba 3:2, 10:12), что является всего лишь выдохом, не требующим никаких усилий. Подражая своему Творцу, природа прилагает как можно меньше усилий при выборе пути движения. Это духовная версия принципа наименьшего действия.
Примечания:
[1] Евклид, греческий математик, живший около 300 г. до н. э., был самым знаменитым геометром и логиком древности, которого считают отцом геометрии. Он наиболее известен своим трактатом Elements, который заложил основы геометрии.
[2] Catoptrica, также известная как Catoptrics, — это работа Евклида, посвященная математической теории зеркал.
[3] Угол падения — это угол между входящим лучом света и перпендикулярной линией к отражающей поверхности. Угол отражения — это угол между отраженным лучом света и той же перпендикулярной линией.
[4] Макс Хельцбергер, «Оптика от Евклида до Гюйгенса», Applied Optics, 1966, 5 (9), стр. 1383–93.
[5] Герон Александрийский, также известный как Герон из Александрии, был греческим математиком и инженером, жившим около 60 г. до н. э. В математике он больше всего запомнился формулой Герона для вычисления площади треугольника, используя только длины его сторон.
[6] Моррис Клайн, Mathematical Thought from Ancient to Modern Times. (Нью-Йорк: Oxford University Press, 1972) стр. 167–68.
[7] Готфрид Вильгельм (фон) Лейбниц (1646–1716) был немецким математиком, философом и ученым. Он является очень важной фигурой как в истории философии, так и в истории математики и физики.
[8] Р. П. Фейнман, Р. Б. Лейтон и М. Сэндс, Фейнмановские лекции по физике, Том II. Калифорнийский технологический институт, 1964, глава 26, «Принцип наименьшего времени».
[9] Ричард Фейнман, Feynman Lectures, Lecture 26, Optics:The Principle of Least Time. (См. онлайн, https://www.feynmanlectures.caltech.edu/I_26.html#:~:text=With%20Snell’s%20theory%20we%20can,on%2C%20is%20easy%20to%20understand.)
[10] Талмуд, тр. Eruvin, 53a.
[11] Рабби Шнеур Залман из Ляди, (Алтер Реббе), Тания, Likutei Amarim, титульный лист.
[12] Талмуд, тр. Tamid 27b.
[13] Medrash Rabba on Genesis, 20, ch. 3. See my earlier essay, “On the Nature of Time and the Age of the Universe,” (2005) (https://quantumtorah.com/on-the-nature-of-time-and-the-age-of-the-universe/).
[14] See my essays, “Space – Between Future and Past,” (June 13, 2019), (https://quantumtorah.com/space-between-future-and-past/)” and “Time as a Combination of Past and Future,” (June 30, 2023) (https://quantumtorah.com/time-as-a-combination-of-past-and-future/).
[15] «И животные бежали и возвращались, как вид молнии». (Иезекииль 1:14). См. мое эссе «Cosmic Symphony», QuantumTorah.com, 30 октября 2019 г., https://quantumtorah.com/cosmic-symphony/.
[16] Иоганн Бернулли (1667–1748), выдающийся швейцарский математик, учитель Леонарда Эйлера. Бернулли внес значительный вклад в исчисление.
[17] Brachistochrone в переводе с греческого означает «кратчайшее время».
[18] Вариационное исчисление — это область математического анализа, которая использует вариации, то есть небольшие изменения в функциях и функционалах, для поиска максимумов и минимумов функционалов: отображений из множества функций в действительные числа. В то время как элементарное исчисление связано с бесконечно малыми изменениями значений функций без изменений в самой функции, вариационное исчисление связано с бесконечно малыми изменениями в самой функции, которые называются вариациями (Рихард Курант и Дэвид Гильберт, Methods of Mathematical Physics. (Нью-Йорк: Interscience Publishers, Inc. 1953), Vol. I, p. 184.
[19] Пьер-Луи Моро де Мопертюи, Essai de Cosmologie, 1750.
[20] Леонард Эйлер (1707–1783), швейцарский математик, логик, физик, астроном и инженер. Он считается одним из величайших математиков всех времен. Он основал теорию графов и топологию. Он внес глубокий вклад во многие области математики и физики, включая теорию чисел, комплексный анализ, исчисление, механику, гидродинамику, оптику и астрономию. Он также внес вклад в теорию музыки.
[21] Леонард Эйлер, Methodus Inveniendi Lineas Curvas Maximi Minimive Proprietate Gaudentes,Lausannae & Genevae: Bousquet & Socios. 1744, 1st edition, art. 1, trans. Ivor Grattan-Guinness.
[22] Жозеф-Луи Лагранж (по рождению Джузеппе Луиджи Лагранжиа, 1736–1813) был выдающимся итальянским математиком, физиком и астрономом, который позже в жизни стал французским гражданином. Он внес важный вклад в области анализа, теории чисел, классической и небесной механики.
[23] Например, Сефер Йецира делит мир на три области — olam («мир,» то есть пространство), shanah («год», то есть время) и nefesh («душа», то есть духовность). (См. Sefer Yetzirah (Книга Созидания), 6:4. Английский перевод см. Aryeh Kaplan, Sefer Yetzirah: The Book of Creation. Weiser Books, 1997.)
[24] Маймонид, Mišneh Torah, Hilḥot De’ot, Chapter 1, Halaḥa 4.
[25] Sifrei end of Ekev.