פוסט זה הוא המשך לפוסט הקודם שלי, “מרחב – בין עתיד ועבר“. לרקע נוסף, הקורא מופנה לפוסט ההוא.
“ההתגלות” השנייה שלי בשבועות הייתה שהמרחב הוא יחסי. לא שהבנתי לראשונה שהמרחב הוא יחסي – תמיד חשבתי כך. אבל, מסיבה כלשהי, החשיבה על המשמעות של ארבעת הפנים של החיות, “הברואים החיים” – הישויות המלאכיות המתוארות בנבואתו של יחזקאל שאנו קורא בשבועות – הבהירה זאת לחלוטין במוחי.
הדיון על טבע המרחב חוזר לפחות לתקופות של ניוטון וליבניץ. יצחק ניוטון האמין (כפי שניכר ממכניקה שלו וכפי שביטא חברו, שמואל קלארק) שהמרחב הוא מוחלט ולכן, אפשר לדבר על מרחב ריק. גוטפריד וילהלם ליבניץ, מצד שני, האמין שהמרחב ניתן לצמצום ליחסים בין עצמים. יצחק ניוטון דמיין את המרחב כרקע של העולם, הבמה עליה מתגלגל המחזה הקוסמי, הקנווס עליו מצויר הציור.
אלברט איינשטיין לא הסכים עם ניוטון שהמרחב הוא נוקשה ומוחלט. לפי איינשטיין, המרחב היה עמיל וניתן לעיוות ועיקום על ידי תנועה וכבידה. אולם, איינשטיין עדיין דמיין אותו כמרקם הבסיסי של היקום – חלק ואוניברסלי – ובמובן זה, תורת היחסות הכללית מציגה לנו מרחב מוחלט הקיים אפילו ביקום ריק מכל חומר. מעולם לא יכולתי להזדהות עם זה. בעקבות ליבניץ, תמיד חשבתי שהמרחב הוא רק סכום כולל של כל היחסים בין עצמים שונים.
תדמיינו יקום ריק או יקום עם חלקיק יחיד בו. האם באמת יכולנו לדבר על מרחב בתרחיש זה? אינני חושב כך. אין דרך לדבר על מיקומו של החלקיק הבודד הזה מכיוון שאין חלקיק אחר לבחור כמרכז מערכת הקואורדינטות. אין עצם אחר ביחס אליו ניתן לתאר את מיקומו של החלקיק הבודד. אם היו לפחות שני חלקיקים, יכולנו לדבר על המרחק ביניהם, מכיוון שיכולנו לחבר אותם בקו דמיוני. אם היו שלושה חלקיקים או יותר, יכולנו לחבר כל חלקיק עם כל חלקיק אחר, ולמדוד לא רק מרחקים ביניהם אלא גם זוויות.
כל שלושה חלקיקים יכולים ליצור רקע של מרחב דו-ממדי. כמה רקעים כאלה “מודבקים” יחד, יוצרים מרחב תלת-ממדי שיכול, באופן עקרוני, להיות בעל עקמומיות. זהו החומר ממנו עשויה הגיאומטריה, וכך, במוחי, נולד המרחב.
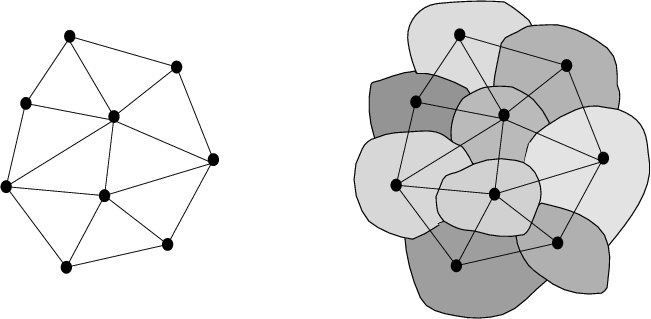
שני פיזיקאים תיאורטיים, קארלו רובלי ולי סמולין, שניהם שאני מעריץ מאוד, היה להם אותו רעיון כמו ליבניץ. הם לקחו אותו הרבה יותר רחוק ונתנו לו בסיס מתמטי, קצף סיבוב. הם יצרו מחדש גיאומטריה מתוך בלגן של קווים המחברים כל עצם עם כל עצם אחר ביקום.
מרחב-הזמן היחסי שלהם הפך ליסוד תורת כבידה הלולאות הקוונטית, אחת המתמודדות המובילות לתורת קוונטים של כבידה, הגביע הקדוש של הפיזיקה התיאורטית.
כפי שאמרתי בפוסט הקודם שלי, “מרחב – בין עתיד ועבר“, הז”א (פרצוף זעיר אנפין), שהוא המקור הרוחני של המרחב התלת-ממדי שלנו, מתאים לאות ו’ בתטראגרמטון, שיש לה ערך גימטריה של 6, המתאים לשש הכיוונים במרחב תלת-ממדי.
| אות | עבר. אות | ספירה עיקרית | פרצוף | זמן |
| יוד | י | חכמה | אבא | עבר |
| הא | ה | בינה | אימא | עתיד |
| ואו | ו | שש ספירות | זעיר אנפין | הווה |
אולם, האות העברית ו’ היא רק קו אנכי – ו. בעיני, הצורה הוויזואלית הזו של האות המתאימה למרחב היא אינדיקציה שהמרחב התלת-ממדי שלנו הוא רשת של קווים המחברים עצמים במרחב.
אם זה לא מספיק, בואו נבחן את המשמעות של האות ו’ – ו. בעברית, האות ו’ (לפעמים גם מתועתקת כוו) היא מחברת – משמעותה המילולית היא “ו”. לדוגמה, כשאנחנו רוצים לומר, רחל ולאה, אנחנו אומרים בעברית רחל ולאה עם האות ו’ (מבוטאת כ”ו”) המשמשת כחיבור “ו”. אז, במובן הסמנטי הזה, האות ו’ היא מחברת המיוצגת גרפית על ידי קו. כשיש לנו מספר עצמים ביקום – עצם 1, עצם 2, עצם 3, וכו’ – הפועלים איכשהו זה עם זה, אנחנו מקבצים אותם יחד באומרם עצם 1 ועצם 2 ועצם 3, וכו’. בעברית, משתמשים באות ו’ הכתובה כקו אנכי במקום ה”ו” האנגלית. אם נחבר שלושה עצמים לא קוליניאריים יחד בקווים ישרים, אותיות ו’, נקבל משולש. אם נחבר ארבע נקודות לא קופלנריות בקווים ישרים, אותיות ו’, נקבל את ה-3-סימפלקס או הטטרהדרון. זהו ייצוג חי של איך עצמים ביקום מחוברים בקווים דמיוניים המייצגים אינטראקציות בין העצמים (בפיזיקה אנחנו קוראים לזה “צימוד”). מכל הקווים האלה, נולד המרחב.
בפוסט הקודם שלי, “מרחב – בין עתיד ועבר“, כתבתי שהמרחב קיים “בין” העתיד לעבר והוא זהה לרגע הנוכחי. אם כך, המרחב נברא מחדש עם כל רגע חדש.
אתם אולי תוהים, איך יכול המרחב שלנו להיברא מחדש או “להתרענן” בכל רגע? אם המרחב היה קנווס, החלפת הקנווס פוטרת מהציור! באופן דומה, אם המרחב היה מכל לעצמים שבו (מכל הוא מטפורה נפוצה למרחב מוחלט), הרס המכל היה הורס את כל העצמים שבו! אולם איננו רואים שזה קורה – העצמים לא נעלמים בכל רגע. עתה נוכל להבין מדוע.
אם המרחב אינו אלא קבוצה של יחסים בין עצמים, יצירה מחדש של מרחב כזה פירושה פשוט עדכון היחסים האלה. אם עצמים נעים מרגע אחד לאחר, קו אחד יהפוך ארוך יותר, אחר קצר יותר, חלק מהזוויות בין הקווים ישתנו; כל היחסים הגיאומטריים יתעדכנו מבלי לגעת בעצמים עצמם. רענון הקשרים בין עצמים אינו הורס את העצמים.
מה טבעם של הקווים האלה שמרכיבים את המרחב? קווים מייצגים יחסים בין עצמים. יתרה מכך, מכיוון שהאות ו’ פירושה מחברת, היא רומזת על טבע היחסים האלה כקשרים. כפי שהצעתי קודם, היחסים או הקשרים האלה מייצגים אינטראקציות פיזיקליות בין עצמים. אבל אילו אינטראקציות?
“ההתגלות” הנוספת שלי הייתה ההבנה שהקווים האלה מייצגים משיכה כבידתית. אכן, כבידה היא אינטראקציה אוניברסלית במובן שכל העצמים יש להם אנרגיה/מסה ולכן, מפעילים (ומגיבים ל) משיכה כבידתית. כך, המרחב הוא כבידה, והכבידה היא מרחב.
לעתים קרובות נאמר בספרות הפופולרית שאיינשטיין השווה בין מרחב-זמן לכבידה. לדעתי, זה אינו נכון. תורת היחסות הכללית מנוסחת על גבי יריעה פסאודו-רימנית דיפרנציאלית קיימת מראש. לפי איינשטיין, המשוואות של השדה הכבידתי מדגימות כבידה כעקמומיות של מרחב-הזמן – מסה מעקמת את מרקם מרחב-הזמן. במילותיו של ג’ון ארצ’יבלד וילר, מסה אומרת למרחב איך להתעקם והמרחב אומר למסה איך לזוז. כבידה, לפי איינשטיין, היא המתיחה והכיפוף של מרקם מרחב-הזמן, אך לא המרקם עצמו. בניסוח שלי של תורת היחסות הכללית שהצעתי ב-1979, כבידה תוארה כעיוות אפיני של מרקם מרחב-הזמן. שתי הגישות מניחות קיום מוקדם של מרחב-זמן כרקע לשדה הכבידתי.
אני חושב עתה שכבידה היא המרחב עצמו (לא מרחב-זמן ארבע-ממדי, אלא מרחב תלת-ממדי). לא המרחב החלק של תורת היחסות הכללית, אלא המרחב הדיסקרטי המורכב מרשת של קווים המחברים את כל העצמים ביקום.
את כל זה הבנתי בזמן שחשבתי על ישויות מלאכיות, חיות, וארבעת פניהן בנבואתו של יחזקאל, מעשה המרכבה שאנו קוראים בשבועות.
