עשר ספירות ותורת היחסות הפרטית

התיאוריה המיוחדת של היחסות, שפורסמה על ידי אלברט איינשטיין בשנת 1905, הייתה פורצת דרך. היא פתחה את עידן הפיזיקה החדשה שכונתה על ידי חלק מהאנשים כ”פיזיקה יהודית”. ואכן, זו הייתה פיזיקה יהודית.

בליבה של תורת היחסות הפרטית נמצא מושג היחסיות של התנועה – כל תנועה אינה מוחלטת, כפי שניוטון חשב, אלא יחסית למשהו אחר, לנקודת מבט מסוימת. בפיזיקה, אנו מגדירים נקודת מבט כמערכת ייחוס. אם אתה עומד ברכבת נוסעת, העוזבת את רציף הרכבת, במערכת הייחוס שלך (שתמיד במנוחה) הרכבת נמצאת במנוחה ביחס למערכת הייחוס שלך. רציף הרכבת, מצד שני, נע ביחס למערכת הייחוס שלך. עבור מישהו העומד על הרציף ומנופף לשלום, רציף הרכבת כמובן במנוחה, והרכבת ואתה מתרחקים במהירות – הכל יחסי.

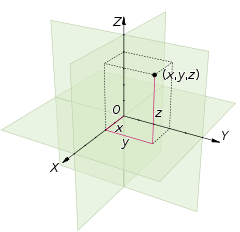
מתמטית, התיאוריה המיוחדת של היחסות מתארת מערכות ייחוס כמערכות קואורדינטות במרחב-זמן ארבע-ממדי הנקרא מרחב מינקובסקי. מלבד שלושת הממדים המרחביים המוכרים x, y, z, (או למעלה-למטה, קדימה-אחורה, וימינה-שמאלה):

היא מוסיפה את הממד הרביעי הזמני t.

חוקי הטבע צריכים להיות בלתי משתנים ביחס לטרנספורמציית קואורדינטות. משמעות הדבר היא שלא משנה באיזו מערכת קואורדינטות תבחר, זה לא אמור להשפיע על חוקי הטבע – הם זהים בכל נקודה במרחב ובכל רגע בזמן. במתמטיקה, זה נקרא סימטריה.

סוג אחד של סימטריה במרחב הוא סימטריה סיבובית. אם נסובב את מערכת הקואורדינטות שלנו סביב ציר, נניח ציר ה-z, זה אמור להשאיר משהו ללא שינוי. אותו משהו הוא וקטור במרחב מינקובסקי. הרמן מינקובסקי היה מורה המתמטיקה של איינשטיין בקולג’, שהציע לראשונה לאחד את המרחב והזמן לרצף מרחב-זמן ארבע-ממדי, העולם, כפי שהוא קרא לו.

סיבובים סביב ציר של מערכת הקואורדינטות משאירים את הגודל והכיוון של וקטור ללא שינוי, או בשפה המתמטית, בלתי משתנים. כל טרנספורמציות הקואורדינטות במרחב מינקובסקי נקראות טרנספורמציות לורנץ על שם הנדריק אנטון לורנץ, פיזיקאי הולנדי שתיאר לראשונה מתמטית את התארכות הזמן והתכווצות האורך במהירויות גבוהות. מכיוון שיש שלושה צירים מרחביים שסביבם אנו יכולים לסובב את הקואורדינטות, יש שלושה סיבובי לורנץ כאלה.

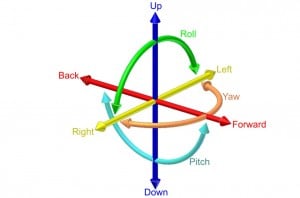
סוג נוסף של סימטריה הוא האצת לורנץ – המעבר ממערכת ייחוס אחת למערכת ייחוס אחרת הנעה במהירות קבועה לאורך קו ישר. מכיוון שמערכת כזו יכולה לנוע ביחס למערכת הייחוס שבחרנו בשלושה כיוונים שונים, יש שלוש האצות לורנץ כאלה.

כל הטרנספורמציות כאלה שמשאירות וקטור של מרחב מינקובסקי בלתי משתנה מרכיבות את מה שנקרא קבוצת לורנץ. מכיוון שיש שישה סוגים של טרנספורמציות כאלה – שלושה סיבובים ושלוש האצות – לקבוצת לורנץ יש שישה פרמטרים או שישה ממדים.

מלבד סיבובים והאצות, ישנן טרנספורמציות קואורדינטות אחרות – העתקות – כאשר אנו מזיזים את כל מערכת הקואורדינטות לאורך אחד מארבעת הצירים (בשלושה כיוונים במרחב ובזמן). ארבע ההעתקות האלה שמשאירות את גודל הוקטור בלתי משתנה (אם כי הן מזיזות את הוקטור למקום אחר) כאשר מוסיפים אותן לקבוצת לורנץ מרחיבות אותה למה שנקרא קבוצת פואנקרה. אנרי פואנקרה היה מתמטיקאי צרפתי שתרם להתפתחות תורת היחסות הפרטית.

מכיוון שיש ארבעה צירים – שלושה מרחביים ואחד זמני – יש ארבעה פרמטרים נוספים בקבוצת פואנקרה. יחד עם ששת הפרמטרים של קבוצת לורנץ, לקבוצת פואנקרה יש סך הכל עשרה פרמטרים או עשרה ממדים. הבה נסכם פרמטרים אלה בטבלה הבאה

קבוצת פואנקרה

לחלופין, אנו יכולים לקבץ פרמטרים אלה כך

קבוצת פואנקרה מתארת את כל הסימטריות ולכן את הגיאומטריה של מרחב מינקובסקי. הודות למשפט נתר המפורסם שנוסח על ידי המתמטיקאית היהודייה-גרמנייה אמלי אמי נתר, אנו יודעים כעת שכל סימטריה מתאימה לחוק שימור פיזיקלי. לדוגמה, הסימטריה ההעתקתית אחראית לשימור התנע, הסימטריה הסיבובית אחראית לשימור התנע הזוויתי, וסימטריית הזמן אחראית לשימור האנרגיה. לכן, קבוצת פואנקרה לא רק מגדירה את הגיאומטריה של היחסות אלא גם את הפיזיקה שלה. היא היסוד של תורת היחסות ותורת השדה הקוונטית – המודל הסטנדרטי. היא אכן היסוד של הפיזיקה המודרנית.

על פי הקבלה, העולם הפיזי שבו אנו חיים הוא השתקפות של עולמות רוחניים גבוהים יותר בעלי מבנה דומה. הגיוני להניח, לפיכך, שלמרחב ולזמן הרוחניים בעולמות הרוחניים שמעלינו יש את אותה גיאומטריה כמו לעולם הפיזי שלמטה. אם העולם הפיזי הוא רק השתקפות של הממד הרוחני, עלינו לצפות למצוא את קבוצת פואנקרה במרחב הרוחני.

הקבלה מלמדת אותנו שמבנה העולמות הרוחניים בנוי סביב עשר ספירות. (מעט דברים מרגיזים אותי יותר מאשר כאשר אנשים משווים את עשר הספירות לעשרה ממדים בתורת המיתרים. זו אנלוגיה מאולצת – מלבד המספר עשר, אין להם שום דבר במשותף!)

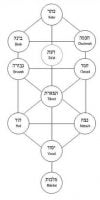
רק העובדה שיש עשר ספירות ועשרה פרמטרים של קבוצת פואנקרה לא תספיק כדי לערוך אנלוגיה. אבל הבה נתבונן במבנה של עשר הספירות:

עשר הספירות

או, לחלופין,

לעתים, ארבע האצילויות התחתונות, נצח, הוד, יסוד, מלכות, מקובצות יחד. לדוגמה, כאשר דנים בהבדלים בין שבת, שנת השמיטה, שמיטה, והיובל, יובל, האר”י אומר שבמהלך השבת, ארבע הספירות התחתונות – נצח, הוד, יסוד, מלכות (נהי”מ – מבוטא נהים) מתעלות יחד (ראה ספר ליקוטים, בהר). בלשון הזוהר, ארבע הספירות התחתונות הללו מרכיבות את “הגוף התחתון”.

אם עדיין לא שמתם לב לדמיון, הבה אביא עכשיו את עשרת הפרמטרים של קבוצת פואנקרה ועשר הספירות יחד:

לחלופין,

אנו רואים שגם קבוצת פואנקרה וגם עשר הספירות ניתנות להצגה כשלוש שלשות בתוספת האלמנט העשירי, שבקבוצת פואנקרה הוא תרגום בזמן ובספירות הוא מלכות. הקבלה מלמדת שהזמן מגיע ממלכות (של עולם האצילות – אצילות). לחלופין, ניתן להציג את שני המבנים כשתי שלשות ורביעייה – ארבעה תרגומים בקבוצת פואנקרה המקבילים לארבע הספירות התחתונות שנעות (מתרגמות) יחד בשבת. שלוש הספירות הראשונות, חכמה, בינה, ודעת (חב”ד) מקבילות לשלושה סיבובים סביב צירי X, Y, ו-Z. השלשה השנייה של הספירות, חסד, גבורה, ותפארת (חג”ת) מקבילות לשלושה האצות לורנץ. וארבע הספירות התחתונות, נצח, הוד, יסוד, ומלכות (נהי”מ) מקבילות לארבעה תרגומים במרחב מינקובסקי. כך, ניתן לראות את עשר הספירות כעשרה פרמטרים (או ממדים) של קבוצת פואנקרה. הכל מתחבר כעת.

הדמיון המבני המפתיע הזה מרמז שאכן, כפי שבמרחב הפיזי קבוצת פואנקרה מגדירה את הגיאומטריה, במרחב הרוחני, עשר הספירות מגדירות עשרה פרמטרים (או ממדים) ואת המבנה של קבוצת פואנקרה. אכן, פיזיקה יהודית!