מחזה היקום נעשה כה גדול יותר, כה יפה יותר, ראוי יותר ליוצרו, כאשר יודעים שמספר קטן של חוקים, שנקבעו בחוכמה רבה, מספיקים לכל התנועות.
פייר לואי מופרטואי (1744)
מבין החוקים הפחות או יותר כלליים, שגילוים מאפיין את התפתחות המדע הפיזיקלי במאה האחרונה, עקרון הפעולה המינימלית הוא כיום בוודאי זה אשר, בצורתו ובהיקפו, ניתן לומר שהתקרב ביותר למטרה האידיאלית של החקירה התיאורטית. משמעותו, כאשר מבינים אותה כראוי, מתפשטת לא רק לתהליכים מכניים, אלא גם לבעיות תרמיות ואלקטרודינמיות. בכל ענפי המדע שבהם הוא חל, הוא נותן לא רק הסבר למאפיינים מסוימים של תופעות הנתקלות כיום, אלא מספק כללים שבאמצעותם ניתן לקבוע באופן מלא את השינויים שלהן בזמן ובמרחב. הוא מספק את התשובות לכל השאלות הקשורות אליהן, בתנאי שהקבועים הנחוצים ידועים והתנאים החיצוניים הבסיסיים נבחרו כראוי.
מקס פלאנק (1909)
תוכן העניינים
ב. מבוא לעקרון הפעולה המינימלית
III. היסטוריה <— אתה כאן
VII. V. המקור הרוחני של עקרון הפעולה המינימלית
זהו הפרק השלישי בסדרה על עקרון הפעולה המינימלית. בפרק הראשון, “עקרון הפעולה המינימלית I“, הכרנו את הטלאולוגיה. למדנו שטלאולוגיה היא סיבה או הסבר למשהו המשמש כפונקציה של מטרתו, בניגוד למשהו המשמש כפונקציה של סיבתו. שמאמינים שיש לו מטרה, יעד או מטרה שאליהם הוא שואף. מטרת הסוף נקראת הסיבה הסופית (causa finalis). למדנו גם שהיהדות היא ללא ספק טלאולוגית עד היסוד ושהאמונה היהודית מבוססת על האמונה באלוקים בעל מטרה, שיצר עולם בעל מטרה. בפרק השני, הכרנו את עקרון הפעולה המינימלית. למדנו שעקרון הפעולה המינימלית הוא ייצוג פורמלי של רעיונות פשוטים כמו יעילות ואופטימיזציה. הטבע שואף לחקות את בוראו כמיטב יכולתו. לכן, היעילות של הטבע היא ביטוי של שלמות הבורא האינסופי בתוך הגבולות הסופיים של העולם הפיזי. בפרק זה (השלישי), אנו הולכים לסקור את ההיסטוריה של התפתחות עקרון הפעולה המינימלית, מה שיעמיק את הבנתנו של עקרון קרדינלי זה של המדע.
ג׳. היסטוריה
עקרון הפעולה המינימלית הוא עקרון הממלא תפקיד יסודי בניסוח המכניקה הקלאסית (גם מכניקה לגראנז׳יאנית וגם המילטונית), מכניקה רלטיביסטית (גם תורת היחסות המיוחדת וגם הכללית), אלקטרודינמיקה, מכניקת נוזלים, מכניקת הקוונטים, פיזיקת חלקיקים, תורת השדות הקוונטיים ותורת המיתרים. הוא נעשה שימוש גם בביולוגיה, בכלכלה ובתחומים אחרים מחוץ לפיזיקה. התפתחותו ההיסטורית שזורה עמוק בהתקדמות הפיזיקה ובהבנת העולם הטבעי. סקירה קצרה של ההיסטוריה שלו עשויה לעזור לנו לפתח הבנה אינטואיטיבית עמוקה יותר של עקרון זה.
1. העת העתיקה

איור 3. אוקלידס מאת חוזה דה ריברה, בערך 1630–1635 (ויקיפדיה, רשות הציבור)
הזרעים המוקדמים ביותר של הרעיון ניתן למצוא ביוון העתיקה. אוקלידס[1] כתב בקטופטריקה[2] שלו שעבור נתיב האור המשתקף ממראה, זווית הפגיעה שווה לזווית ההשתקפות,[3] מה שמרמז שקרן האור נוסעת לאורך הנתיב הקצר ביותר—קו ישר.[4]
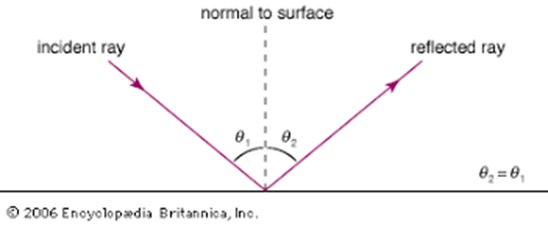
הרון מאלכסנדריה[5] במאה ה-1 לספירה תיאר במפורש את “חוק ההשתקפות” באמצעות מושג “הנתיב הקצר ביותר”.[6] זהו רמז מוקדם לעקרונות וריאציוניים בפיזיקה.

איור 4. תיאור גרמני מהמאה ה-17 של הרון מאלכסנדריה (ויקיפדיה, רשות הציבור).
מנקודת מבט תיאולוגית, בחירת הדרך הנכונה—דרך הישר (“הדרך הישרה”) היא מצוווה דתית. לדוגמה, אנו מוצאים במשלי:
בכל דרכיך דעהו והוא יישר אורחותיך.
משלי ג׳:ו׳
אנו מוצאים גם את המצווה הזו בתהילים:
הורני יהוה דרכך נחני בארח מישור…
תהילים כ״ז:י״א
כשמתנבא על שובם של הגולים במהלך הגאולה הסופית, ירמיה כותב:
הולכתים אל נחלי מים בדרך ישרה לא יכשלו בה…
ירמיה ל״א:ט׳
הקבלה הלוריאנית מלמדת שלאחר הצמצומים הקדמוניים (צמצום)—ההסתרה הראשונית של האור האלוהי אור אין סוף—יצירת חלל ריק (חלל) לעולם, האלוקים שלח קרן של האור האלוהי לתוך החלל הריק. קרן אור זו נקראת בקבלה, הקו (קו [ישר]). האם זה פלא שהעולם שנוצר על ידי קו הקו הישר הזה מתנהג באופן דומה על ידי בחירת האור הישר כמסלול התנועה המועדף?
2. הרנסאנס
(א) עקרון פרמה

איור 5. דיוקן של פייר דה פרמה על ידי מחבר לא ידוע, מאה 17 (רשות הציבור, ויקיפדיה)
עקרון המרחק המינימלי עובד היטב במקרה מיוחד, כשאור עובר דרך מדיום יחיד. עם זאת, כשאור חוצה שני מדיומים או יותר, כמו אוויר ומים, הוא כבר לא נוסע בקו ישר—עקרון המרחק המינימלי כבר לא עובד במקרה כללי זה. בשנת 1662, המתמטיקאי הצרפתי פייר דה פרמה הציע את “עקרון הזמן המינימלי” להתפשטות אור, הידוע כיום באופטיקה כעקרון פרמה. הוא הציע שאור נוסע בין שתי נקודות לאורך הנתיב הדורש את הזמן הקצר ביותר. הוא קדם בזה על ידי גוטפריד לייבניץ.[7] כדי לחשב את נתיב האור המתפשט דרך שני מדיומים צריך לחשב את זמני האור הנוסע בכל מדיום בנפרד (כי אור נוסע במהירויות שונות במדיומים שונים) ואז למזער את הזמן הכולל, מה שייתן את זווית השבירה. עקרון הזמן המינימלי מכליל את עקרון המרחק המינימלי.

איור 6. גוטפריד וילהלם לייבניץ, מאת כריסטוף ברנהרד פראנקה, 1695 (ויקיפדיה, רשות הציבור)
כדי לפתח הבנה אינטואיטיבית של עקרון פרמה, בואו נניח שאתה אוהב לרכוב על אופניים לעבודה ושואף להגיע למשרד שלך בזמן הקצר ביותר האפשרי. יש שתי דרכים למשרד שלך—אחת נתיב ישר שטח חוצה מדשאות עשבוניות וכתמי בוץ, ואחרת הוא כביש סלול שהוא ארוך יותר אבל לא חסום. בעקבות עקרון הרון של הנתיב הישר, היית בוחר בנתיב הישר השטח ומגיע למשרד מאוחר. הליכה בכביש סלול אם כי ארוך יותר תביא אותך למשרד מהר יותר.
דוגמה אחרת, ואולי טובה יותר, ניתנה על ידי ריצ׳רד פיינמן בהרצאות שלו. נניח, מציל שצופה בשחיינים על חוף מבחין במישהו שטובע באוקיינוס. הוא לא הולך לקפוץ מיד לאוקיינוס אלא קודם ירוץ לאורך החוף לפני הכניסה למים, כי הוא יודע שריצה על משטח יבש מהירה יותר משחייה במים. המטרה היא להגיע לאדם הטובע כמה שיותר מהר—כלומר, למזער את הזמן הכולל. [8]
בחירה אפריורי בנתיב שלוקח זמן מינימלי, יש גוונים טלאולוגיים חזקים. ריצ׳רד פיינמן הדגיש זאת בהרצאות המפורסמות שלו:
הרעיון של סיבתיות, שהיא עוברת מנקודה אחת לאחרת, ואחרת, וכן הלאה, קל להבנה. אבל עקרון הזמן המינימלי הוא עיקרון פילוסופי שונה לחלוטין על האופן שבו הטבע פועל. במקום לומר שזה דבר סיבתי, שכאשר אנו עושים דבר אחד, משהו אחר קורה, וכן הלאה, הוא אומר זאת: אנו מגדירים את המצב, והאור מחליט מהו הזמן הקצר ביותר, או הקיצוני ביותר, ובוחר במסלול הזה. אבל מה הוא עושה, איך הוא מגלה? האם הוא מריח את המסלולים הסמוכים, ובודק אותם זה מול זה?[9]
התלמוד מספר את סיפורו של רבי יהושע הפוגש ילד צעיר בצומת דרכים. רבי יהושע שאל את הילד איזו הדרך לעיר, והילד סיפר לו על שתי דרכים – דרך קצרה אך ארוכה ודרך ארוכה אך קצרה. רבי יהושע בחר תחילה בדרך הקצרה אך הארוכה, שהייתה קצרה יותר במרחק אך היו בה מכשולים שהאריכו את המסע. אז הבין את דברי הילד. יש דרכים ארוכות יותר, שהן המהירות ביותר.[10] רבי שניאור זלמן מליאדי בחר בביטוי זה – דרך ארוכה אך קצרה יותר – כאפיגרף לתניא שלו.[11]
מנקודת המבט של ההלכה היהודית, Halachah, עקרון הזמן המינימלי נראה עדיף על פני עקרון המרחק המינימלי. התלמוד דן במצב שבו כהן נטמא (טומאה) בעודו בבית המקדש.[12] אסור לכהן להיות בבית המקדש במצב של טומאה (טומאה טקסית). האם עליו לחפש את הדרך הקצרה ביותר או המהירה ביותר לצאת מהשטח הקדוש? לדוגמה, הוא עשוי לראות שני שערים המובילים החוצה, אחד קרוב אליו והשני רחוק יותר. הוא רואה המונים נכנסים לשטח בית המקדש מהשער הקרוב ומבין שאם ירוץ לכיוון השער הקרוב, הוא יואט משמעותית על ידי ההמונים הנעים בכיוון ההפוך – הוא ירוץ נגד הזרם. השער הרחוק יותר פנוי, ללא המונים בינו לבין השער. ברור שבניסיון למזער את זמן נוכחותו הבלתי מותרת על האדמה הקדושה, הכהן סביר להניח שירוץ לשער הרחוק יותר, כי זה ייקח פחות זמן להגיע אליו.
מנקודת המבט של הקבלה, נראה מתאים להכליל את עקרון המרחק הקצר ביותר עם עקרון פרמה. בהיררכיה הרוחנית של הקבלה, הזמן מופיע “לפני” המרחב. בעולם האצילות (העולם הרוחני הגבוה ביותר), שש המידות (הספירות התחתונות) – חסד, גבורה, תפארת, נצח, הוד, ויסוד – מרכיבות את סדר הזמנים – הקדמון של הזמן. [13] המרחב, שמופיע נמוך יותר בעץ הספירות במלכות של אצילות, יורש את אותו המבנה, כאשר שש מידות יוצרות שישה כיוונים (ארבעת כיווני המצפן בתוספת למעלה ולמטה) במרחב התלת-ממדי שלנו. יתרה מזאת, במטאפיזיקה של הפילוסופיה החסידית של חב”ד, המרחב מזוהה עם ההווה ה”כרוך” בין העבר לעתיד.[14] המרחב, במובן מסוים, מקורו בזמן. אכן, הזמן מוגדר כשינוי והמרחב כהיעדר שינוי (יציבות, קביעות). עם זאת, השינוי הוא הראשוני, לא הקביעות. הבריאה עוקבת אחר הקצב של רצוא ושוב (ריצה וחזרה).[15] כתוצאה מכך, קביעות היא מצב לא טבעי הן לעולמות הרוחניים והן לפיזיים. מכאן נובע שהזמן הוא ראשוני והמרחב משני. אם עקרון המרחק הקצר ביותר מוגבל למדיום יחיד, כאשר מתייחסים למקרה כללי יותר של מדיה מרובה, טבעי רק להסתכל על המציאות הגבוהה יותר מהמרחב, כלומר הזמן, כדי לחפש הכללה של עיקרון זה. לכן, החלפת המרחק הקצר ביותר בזמן הקצר ביותר עשויה לשקף את התפיסה הקבלית שבמקורו הרוחני, הזמן הוא מושג גבוה יותר מהמרחב ובמובן מסוים, מקיף את המרחב.
(ב) חשבון וריאציות
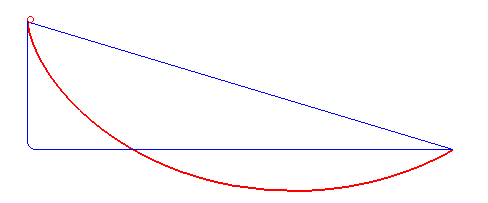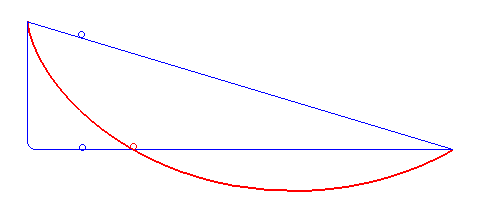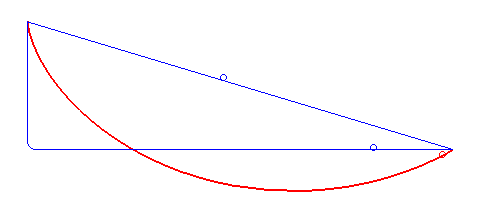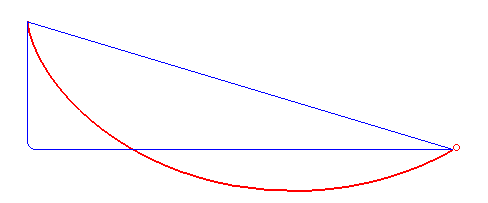
איור 7. עקומת הירידה המהירה ביותר אינה קו ישר או מצולע (כחול) אלא ציקלואיד (אדום). מאת רוברט פרול (נחלת הכלל, ויקימדיה)

איור 8. יוהאן ברנולי מאת יוהאן רודולף הובר, בערך 1740 (נחלת הכלל, ויקימדיה)
בשנת 1696, יוהאן ברנולי[16] הציג את בעיית הברכיסטוכרון[17]: “מהי צורת העקומה שלאורכה חרוז, תחת כוח הכבידה בלבד, יחליק (ללא חיכוך) מנקודה אחת לאחרת בזמן הקצר ביותר?” הפתרון לבעיה זו שהוצע על ידי יוהאן ואחיו ושותפו, יעקב ברנולי, וכן על ידי אייזק ניוטון ואחרים, השתמש בעקרון הווריאציה. הם עזרו לפתח את חשבון הווריאציות כדיסציפלינה מתמטית. [18]
(ג) עקרון הפעולה המינימלית
במאה ה-18, בסביבות 1746, המתמטיקאי והפיזיקאי הצרפתי פייר-לואי מורו דה מופרטואי הציע את עקרון הפעולה המינימלית, המציע שהטבע פועל באופן שממזער כמות מסוימת הקשורה לפעולה. כפי שאמר בפורסם, “הטבע חסכוני בכל פעולותיו.” בעוד שהניסוח של מופרטואי לא היה כללי לחלוטין או נכון לגמרי, הוא הציג את הרעיון שעקרונות וריאציוניים כאלה עשויים לתאר את הטבע.

איור 9. פייר לואי מורו דה מופרטואי, תחריט מאת ז’. דולה, 1741, על פי ר. לברק-טורנייר, 1737 (נחלת הכלל, ויקימדיה)
כפי שהוזכר קודם, מתמטית, העיקרון הווריאציוני מבוטא בנוסחה פשוטה:
δS = 0
בדיוק כמו בחשבון דיפרנציאלי רגיל, הנגזרת המתאפסת מסמנת את הערך הקיצוני (מינימום או מקסימום) של הפונקציה, בחשבון וריאציות, הווריאציה המתאפסת מסמנת את הערך הקיצוני (מינימום או מקסימום) של הפונקציונל S (פעולה).
מעניין לציין שמופרטואי לא התכוון לפתח גישה חדשה לפיזיקה. הוא פיתח את עקרון הפעולה המינימלית שלו, שפורסם ב-1750 בחוברת דקה בשם “מסה על הקוסמולוגיה”, במטרה היחידה להוכיח את קיומו של הקב”ה. הוא כתב:
חוקי התנועה והמנוחה הנגזרים מעיקרון זה הם בדיוק אותם חוקים הנצפים בטבע, אנו יכולים להתפעל מיישומו לכל התופעות. תנועת בעלי החיים, הצמיחה הצמחית של צמחים … הם רק תוצאותיו; ומחזה היקום נעשה כה גדול יותר, כה יפה יותר, ראוי יותר ליוצרו, כאשר יודעים שמספר קטן של חוקים, שנקבעו בחוכמה רבה, מספיקים לכל התנועות. [19]
ציטוט זה מצביע על האופן שבו מופרטיוס חיבר את העיקרון שלו עם הרעיון של קוסמוס גדול ומסודר באופן אלוהי. הוא האמין שכמה חוקים פשוטים ואלגנטיים שנקבעו שלטו בכל התנועות והתופעות ביקום, וזה היה עדות לחוכמת הבורא. למרות שהחוברת שלו זכתה ללעג מצד אינטלקטואלים בני זמנו, בסופו של דבר, המתמטיקה שלו הניחה את היסודות של הפיזיקה המודרנית. אני מאמין שכשם שמופרטיוס היה צודק במתמטיקה שלו, כך הוא צודק בייחוס האחדות והאלגנטיות של העיצוב לחוכמת הבורא.
ההצעה שהטבע פועל באופן כזה שממזער כמות מסוימת היא טלאולוגית בהגדרה—ההתנהגות הפיזיקלית מוסברת על ידי הנחת מטרה, סיבה סופית.

איור 10. לאונהרד אוילר מאת יעקב עמנואל האנדמן (נחלת הכלל, ויקימדיה)
לאונהרד אוילר,[20] אחד המתמטיקאים הפוריים ביותר בהיסטוריה, תרם רבות לפיתוח עיקרון הפעולה המינימלית על ידי ניסוח משוואות התנועה הידועות כיום כמשוואות אוילר-לגראנז’. הוא שילב לעתים קרובות את כתביו המדעיים עם הרהורים תיאולוגיים. הוא האמין בסדר הרציונלי של היקום וראה את יד ה’ בעיצובו.
ב”מכתבים לנסיכה גרמנית” שלו, אוילר כותב על נושאים שונים, נוגע בהרמוניה של היקום ויחסיו עם הבורא. הוא כתב:
מאחר שמבנה היקום הוא המושלם ביותר ומעשה של בורא חכם ביותר, שום דבר כלל לא מתרחש ביקום שבו לא מופיע כלל של מקסימום או מינימום.[21]
קטע זה לוכד את אמונתו של אוילר ביקום מסודר באופן אלוהי שבו חוכמת ה’ ניכרת בשלמות וביעילות של עיצובו.
ז’וזף-לואי לגראנז’[22] גם תרם תרומות יסודיות לחשבון הווריאציות ופיתח עוד יותר את מושג הפעולה המינימלית במכניקה, מה שהוביל לניסוח הלגראנז’יאני של המכניקה הקלאסית.

איור 11. ז’וזף-לואי לגראנז’ (נחלת הכלל, ויקימדיה)
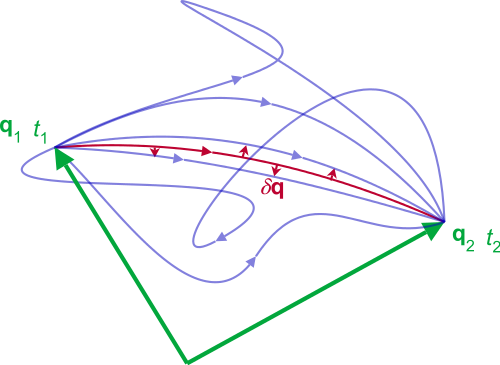
כאשר אנו מחפשים נתיב של חלקיק, כפי שהוא מתפתח מהרגע הראשוני T1 לרגע הסופי T2, טבעי להשתמש בחשבון הווריאציות. המילה העברית שנה (“שנה”) משמשת בדרך כלל כלשון נקיה לזמן.[23] שנה קשורה לשינוי (“שינוי” או “וריאציה”). לפיכך, אנו משנים את הפעולה כדי לקבוע את ההתפתחות בזמן.
דרך נוספת להסתכל על זה מוצעת על ידי הרמב”ם, הקובע ביצירת המופת שלו משנה תורה שהדרך הנכונה היא הדרך האמצעית (דרך האמצעית):
הדרך הנכונה היא האמצע בכל קבוצה של נטיות המשותפות לאנושות; כלומר, אותה נטייה שמרוחקת באופן שווה משני הקצוות בסוגה, ואינה קרובה יותר לאחד מאשר לאחר.[24]
כיצד אנו משיגים את הדרך האמצעית הזו? בקבלה, עץ הספירות מורכב משלושה טורים – הטור האמצעי (כתר, תפארת, יסוד, מלכות), הטור הימני (חכמה, חסד, נצח), והעמודה השמאלית (בינה, גבורה, הוד). באופן אידיאלי, אנו נדרשים לשאוף לדרך האמצע (או העמודה האמצעית). במציאות, עם זאת, אנו מנסים למצוא את דרך האמצע הזו על ידי סטייה קלה לימין, תוך תיקון עצמנו בכל פעם כדי לחזור לאמצע אך מחטיאים את המטרה וסוטים מעט לשמאל, שוב מתקנים את עצמנו כדי לחזור לאמצע, וכן הלאה. תנודה זו בין קצוות מנוגדים בניסיון להשיג את דרך האמצע היא המקבילה הרוחנית לעקרון הווריאציה, שבו אנו משנים את המסלול (נתיב החלקיק) כדי למצוא את הדרך הישרה (או המהירה) ביותר.
זוהי גרסה רוחנית של עקרון הווריאציה.
מקבילה תיאולוגית לעקרון הפעולה המינימלית מבוססת על חיקוי האל. ישנן דרכים רבות לחיות את החיים. איזו דרך עלינו לבחור? התורה מלמדת אותנו שהדרך הנכונה היא לחקות את האל בכל דרכינו.[25] כפי שכתוב:
קדושים תהיו כי קדוש אני ה’ אלוהיכם.
ויקרא י”ט:ב
עלינו להיות צדיקים כי האל צדיק; עלינו להיות טובי לב כי האל טוב לב, וכו’. במרחב המושגי, שבו המרחק נמדד על פי מידת הדמיון, הציווי לחקות את האל יכול להיות מבוטא מתמטית כמזעור המרחק המפריד בינינו לבין האל. ככל שאנו פועלים באופן דומה יותר לאל, כך אנו קרובים יותר אליו. עם זאת, לא רק בני האדם חייבים לחקות את האל; כל הטבע חייב! אכן, אנו מוצאים באיוב:
…ומבשרי אחזה אלוה.
איוב י”ט:כ”ו
“בשר” בפסוק זה הוא לשון נקייה לחומר או לטבע. אנו יכולים לראות את האל בטבע, בעולם החומרי, כי גם הוא מחקה את האל. המדרש אומר שהיה קל לאלוהים לברוא את העולם כפי שקל לנו לבטא את האות ה, האות החמישית באלף-בית (האלפבית העברי), שמבוטאת רק על ידי נשיפה. חז”ל מספרים לנו שהבריאה הייתה ללא מאמץ עבור האל. ( בראשית רבה ג:ב, י:יב), שהיא רק נשיפה שאינה דורשת מאמץ כלל. בחיקוי יוצרו, הטבע משקיע מאמץ מועט ככל האפשר בבחירת מסלול התנועה. זוהי גרסה רוחנית של עקרון הפעולה המינימלית.
הערות שוליים:
[1] אוקלידס, מתמטיקאי יווני, שפרח בסביבות 300 לפנה”ס, היה הגיאומטריקן והלוגיקן המפורסם ביותר בעת העתיקה שנחשב לאבי הגיאומטריה. הוא ידוע בעיקר בזכות חיבורו יסודות, שהניח את היסודות לגיאומטריה.
[2] קטופטריקה, הידועה גם כקטופטריקס היא עבודתו של אוקלידס העוסקת בתיאוריה המתמטית של מראות.
[3] זווית הפגיעה היא הזווית בין קרן האור הנכנסת לבין הקו המאונך למשטח המחזיר. זווית ההחזרה היא הזווית בין קרן האור המוחזרת לבין אותו קו מאונך.
[4] מקס הלצברגר, “אופטיקה מאוקלידס ועד הויגנס,” אופטיקה יישומית, 1966, 5 (9), עמ’ 1383–93.
[5] הרון מאלכסנדריה, הידוע גם כהרון האלכסנדרוני, היה מתמטיקאי ומהנדס יווני, שפרח בסביבות 60 לפנה”ס. במתמטיקה, הוא זכור בעיקר בזכות נוסחת הרון לחישוב שטח משולש באמצעות אורכי צלעותיו בלבד.
[6] מוריס קליין, מחשבה מתמטית מהעת העתיקה ועד לזמנים המודרניים. (ניו יורק: אוניברסיטת אוקספורד פרס, 1972) עמ’ 167–68.
[7] גוטפריד וילהלם (פון) לייבניץ (1646–1716) היה מתמטיקאי, פילוסוף ומדען גרמני. הוא דמות חשובה מאוד הן בהיסטוריה של הפילוסופיה והן בהיסטוריה של המתמטיקה והפיזיקה.
[8] ר. פ. פיינמן, ר. ב. לייטון, ומ. סנדס, הרצאות פיינמן בפיזיקה, כרך. ב׳. המכון הטכנולוגי של קליפורניה, 1964, פרק 26, “עקרון הזמן המינימלי.”
[9] ריצ’רד פיינמן, הרצאות פיינמן, הרצאה 26, אופטיקה: עקרון הזמן המינימלי. (ראה באינטרנט, https://www.feynmanlectures.caltech.edu/I_26.html#:~:text=With%20Snell’s%20theory%20we%20can,on%2C%20is%20easy%20to%20understand.)
[10] תלמוד, מסכת עירובין, דף נג ע”א.
[11] רבי שניאור זלמן מלאדי, (האדמו”ר הזקן), תניא, ליקוטי אמרים, דף השער.
[12] תלמוד, מסכת תמיד דף כז ע”ב.
[13] מדרש רבה על בראשית, כ, פרק ג. ראה את המאמר הקודם שלי, “על טבע הזמן וגיל היקום,” (2005) (https://quantumtorah.com/on-the-nature-of-time-and-the-age-of-the-universe/).
[14] ראה את המאמרים שלי, “חלל – בין עתיד לעבר,” (13 ביוני 2019), (https://quantumtorah.com/space-between-future-and-past/)” ו”זמן כשילוב של עבר ועתיד,” (30 ביוני 2023) (https://quantumtorah.com/time-as-a-combination-of-past-and-future/).
[15] “והחיות רצוא ושוב כמראה הבזק.” (יחזקאל א:יד). ראה את המאמר שלי, “סימפוניה קוסמית,” QuantumTorah.com, 30 באוקטובר 2019, https://quantumtorah.com/cosmic-symphony/.
[16] יוהאן ברנולי (1667–1748), מתמטיקאי שוויצרי בולט, מורהו של לאונרד אוילר. ברנולי תרם תרומה משמעותית לחשבון האינפיניטסימלי.
[17] ברכיסטוכרון ביוונית פירושו “הזמן הקצר ביותר.”
[18] חשבון הווריאציות (או חשבון וריאציוני) הוא תחום בניתוח מתמטי המשתמש בווריאציות, שהן שינויים קטנים בפונקציות ובפונקציונלים, כדי למצוא מקסימום ומינימום של פונקציונלים: מיפויים מקבוצת פונקציות למספרים הממשיים. בעוד שחשבון דיפרנציאלי ואינטגרלי אלמנטרי עוסק בשינויים אינפיניטסימליים בערכי הפונקציות ללא שינויים בפונקציה עצמה, חשבון הווריאציות עוסק בשינויים אינפיניטסימליים בפונקציה עצמה, הנקראים וריאציות (ריצ’רד קורנט ודוד הילברט, שיטות של פיזיקה מתמטית. (ניו יורק: אינטרסיינס פבלישרס, אינק. 1953), כרך I, עמ’ 184.
[19] פייר-לואי מורו דה מופרטואי, מסה על הקוסמולוגיה, 1750.
[20] לאונהרד אוילר (1707–1783), מתמטיקאי, לוגיקן, פיזיקאי, אסטרונום ומהנדס שוויצרי. הוא נחשב לאחד המתמטיקאים הגדולים בכל הזמנים. הוא ייסד את תורת הגרפים והטופולוגיה. הוא תרם תרומות עמוקות לתחומים רבים במתמטיקה ובפיזיקה, כולל תורת המספרים, אנליזה מרוכבת, חשבון אינפיניטסימלי, מכניקה, דינמיקת נוזלים, אופטיקה ואסטרונומיה. הוא גם תרם לתורת המוזיקה.
[21] לאונהרד אוילר, Methodus Inveniendi Lineas Curvas Maximi Minimive Proprietate Gaudentes, לוזאן וז’נבה: Bousquet & Socios. 1744, מהדורה ראשונה, סעיף 1, תרגום איבור גראטן-גינס.
[22] ז’וזף-לואי לגראנז’ (בלידה ג’וזפה לואיג’י לגראנג’יה, 1736–1813) היה מתמטיקאי, פיזיקאי ואסטרונום איטלקי בולט, שבהמשך חייו הפך לאזרח צרפתי. הוא תרם תרומות חשובות לתחומי האנליזה, תורת המספרים, המכניקה הקלאסית והשמימית.
[23] לדוגמה, ספר יצירה מחלק את העולם לשלושה תחומים—עולם (“עולם,” כלומר מקום), שנה (“שנה,” כלומר זמן), ונפש (“נפש,” כלומר, רוחניות). (ראה ספר יצירה (ספר היצירה), ו:ד. לתרגום אנגלי, ראה אריה קפלן, Sefer Yetzirah: The Book of Creation. Weiser Books, 1997.)
[24] רמב”ם, משנה תורה, הלכות דעות, פרק א, הלכה ד.
[25] ספרי סוף עקב.