עץ הדעת כמטאפורה קוונטית-מכנית

למנדל

לפני כמעט שלוש שנים, בדצמבר 2019, פרסמתי מאמר, “עץ הדעת כמטאפורה להטלת-על של מצבים ועקרון אי-הוודאות של הייזנברג”. כתב היד של המאמר הכיל נספח עם מבוא קצר על הטלת-על של מצבים במכניקת הקוונטים וטיפול קוונטי-מכני בחטא הקדמון. הוא ביטא את רעיונותיו של הרמב”ם על החטא הקדמון בנוסחאות מתמטיות מדויקות המוכיחות את ההקבלה המדויקת בין פרי עץ הדעת טוב ורע למחק קוונטי. מתוך הבנה שרק אנשים המכירים את הפורמליזם של מכניקת הקוונטים יבינו חלק זה של המאמר ומחשש לאבד את קוראיי, החלטתי להשמיט את הנספח לחלוטין. עם זאת, הנספח הוא ככל הנראה החלק המעניין ביותר במאמר, מכיוון שהוא מספק דוגמה נדירה לטיפול מתמטי קפדני במושג תיאולוגי המבוסס על הנרטיב המקראי. לבסוף החלטתי לפרסם את המאמר הישן שלי (לאחר עריכה קלה) עם הנספח המתמטי לכבוד יום הולדתו ה-¹⁷ של נכדנו היקר, מנדל. אני מאחל לו הצלחה רבה בלימוד תורה ומכניקת הקוונטים.

***

ויצמח ה’ אלוקים מן האדמה כל עץ נחמד למראה וטוב למאכל ועץ החיים בתוך הגן ועץ הדעת טוב ורע.

בראשית ב:ט

ויצו ה’ אלוקים על האדם לאמר: “מכל עץ הגן אכול תאכל; ומעץ הדעת טוב ורע לא תאכל ממנו, כי ביום אכלך ממנו מות תמות.”

בראשית ב:טז-יז

החטא הקדמון

לאחר בריאת אדם וחוה, התיר להם הקב”ה לאכול מכל פרי בגן עדן, למעט הפרי האסור – פרי עץ הדעת. תוך התעלמות מאיסור זה, אדם וחוה (בעברית, חוה) אכלו מהפרי האסור ושינו לנצח את תולדות העולם. זהו אולי אחד הסיפורים המוזרים ביותר בתורה. ישנן דעות שונות לגבי מהו הפרי האסור – ענבים, תאנה, זית… רובנו אוכלים באופן קבוע ענבים, תאנים וזיתים. אולם, איננו נעשים חכמים יותר או מוסריים פחות מאכילת פירות אלה. כיצד עלינו להבין זאת?

שאלות רבות מבקשות תשובה. מה המשמעות של העץ הנקרא עץ הדעת (בעברית, עץ הדעת)? איזו דעת רכשו אדם וחוה באכילת פריו? מדוע נאסר פרי עץ הדעת? יתרה מזאת, מדוע היה חטא זה כה הרסני עד שהצדיק עונש מוות ואובדן גן עדן?

לפני ביצוע החטא הזה, היה לבני האדם הראשונים חופש בחירה – הם ידעו אמת ושקר, נכון ולא נכון; הם ידעו שאכילת המאכל האסור מעץ הדעת הייתה לא נכונה, כי כך נאמר להם על ידי הקב”ה בעצמו. למעשה, הדבר היחיד שהם ידעו היה אמת (בעברית, אמת) ושקר (בעברית, שקר). המושגים של טוב (בעברית, טוב) ורע (בעברית, רע) היו לא ידועים לאדם וחוה לפני חטא עץ הדעת (חטא עץ הדעת). זו בדיוק הידיעה שהם רכשו באכילת הפרי האסור. כנראה שעץ הדעת נקרא באופן מלא יותר “עץ הדעת טוב ורע” אך ורק משום שהוא היה מקור הידיעה של טוב (טוב) ורע (רע). אכן, בניסיון לשכנע את חוה לאכול מהפרי האסור, הנחש הערמומי מציע זאת כסיבה העיקרית לכך שה’ לא רצה שיאכלו מעץ הדעת טוב ורע:

“כי יודע אלוקים כי ביום אכלכם ממנו ונפקחו עיניכם והייתם כאלוקים יודעי טוב ורע.”

בראשית ג:ה

באכילה מעץ הדעת, רכשו אדם וחוה את הידיעה של טוב (טוב) ורע (רע). מה היה כל כך נורא ברכישת ידיעה זו שהם היו ראויים לעונש מוות? מה לא בסדר בידיעת טוב ורע, וכיצד זה שונה מידיעת אמת ושקר או נכון ולא נכון?

הרמב”ם

בספרו מורה נבוכים (מורה נבוכים), הרמב”ם^[1] מסביר שככל שאדם (וחוה) הבינו טוב יותר את המושגים של טוב ורע, כך הם פחות יכלו להבחין בין אמת ושקר או לשפוט נכון ולא נכון:

…השכל, שניתן לאדם כמתנה העליונה ביותר, הוענק לו לפני מריו. בהתייחס למתנה זו, התורה קובעת ש”האדם נברא בצלם ודמות אלוקים.” . . . באמצעות השכל האדם מבחין בין אמת ושקר. יכולת זו הייתה לאדם באופן מושלם ומלא. . . . ובכן, זהו תפקידו של השכל להבחין בין אמת ושקר – הבחנה שחלה על כל מושאי התפיסה השכלית. . . . כאשר אדם היה עדיין במצב של תמימות, והודרך אך ורק על ידי התבוננות ותבונה . . . הוא לא היה מסוגל כלל לעקוב אחר או להבין את העקרונות של אמיתות נראות לעין [כלומר, סוגיות מוסריות של טוב ורע]; חוסר ההתאמה הבולט ביותר, דהיינו, להופיע במצב של עירום, לא היה דבר בלתי ראוי לפי תפיסתו: הוא לא יכול היה להבין מדוע זה צריך להיות כך. אולם לאחר מרי האדם, כאשר החל להיכנע לתשוקות שמקורן בדמיונו ולסיפוק תאוותיו הגופניות, כפי שנאמר, “ותרא האישה כי טוב העץ למאכל ותאווה הוא לעיניים” (בראשית ג:ו), הוא נענש באובדן חלק מאותה יכולת שכלית שהייתה לו קודם לכן. . . . אז הבין במלואו את גודל האובדן שסבל, מה שהפסיד. . . . בהתבוננו במצבו, אומר המשורר, “אדם ביקר ולא יבין נמשל כבהמות נדמו” (תהלים מט:יג).

מורה נבוכים, חלק א, פרק ב

זה מבלבל מאוד, אכן! הרמב”ם אומר לנו שכל עוד אדם (וחוה, כמובן) קיבלו כוחות שכליים, שהעניקו את היכולת לדעת אמת ושקר ולהבחין בין נכון ולא נכון, אדם וחוה לא יכלו להבין את המושגים של טוב ורע. כלומר, הם לא ראו שום דבר לא בסדר בלהיות עירומים. אולם, לאחר החטא, המצב התהפך – לאחר שרכשו את היכולת לראות טוב ורע (וכתוצאה מכך התביישו בעירומם), איבדו בני האדם הראשונים חלק מכוחם השכלי ואת היכולת לדעת אמת ושקר. כיצד עלינו להבין זאת? מדוע ידיעת טוב ורע מונעת – או מדוע היא אינה מתיישבת עם – ידיעת נכון ולא נכון?

עקרון אי-הוודאות של הייזנברג

הבה נסכם את מה שהרמב”ם אומר: אדם יכול היה לדעת או אמת ושקר (נכון ולא נכון), או טוב ורע, אך לא את שניהם. ככל שלמד יותר את האחרון, כך ידע פחות את הראשון. זה דומה מבחינה מבנית לעקרון אי-הוודאות של הייזנברג במכניקת הקוונטים. ^[2]

מהותו של עקרון אי-הוודאות, שנוסח לראשונה על ידי ורנר הייזנברג ב-1927, היא ששני משתנים משלימים^[3] אינם יכולים להיות ידועים בו-זמנית בדיוק – ככל שאנו מודדים בדיוק רב יותר משתנה אחד, כך המשתנה השני נעשה פחות ודאי. לדוגמה, ככל שאנו יודעים בדיוק רב יותר את מיקומו של חלקיק, כך אנו פחות בטוחים בתנע שלו, ולהפך.^[4] במכניקת הקוונטים, זו תמיד פשרה: ככל שאנו יודעים יותר על תכונה אחת של אובייקט, כך אנו יודעים פחות על התכונה המשלימה האחרת.

בסיפור עץ הדעת, מוצג לנו זוג של תכונות משלימות: אמת ושקר (נכון ולא נכון) מצד אחד, וטוב ורע מצד שני. זו הסיבה שהעץ נקרא עץ הדעת טוב ורע – כי בטעימת פריו רכשו בני האדם הראשונים ידיעת טוב ורע, אך איבדו את ידיעתם של נכון ולא נכון.

הטלת-על של מצבים

נגענו בהטלת-על קוונטית קודם לכן בפוסטים רבים, כולל “שתי התחלות“. הבה נבחן עתה מקרוב יותר את הטלת-העל של מצבים במכניקת הקוונטים.

בספרו, מכניקת הקוונטים וחוויה,^[5] דיוויד אלברט נותן את הדוגמה הבאה, כפי שמובאת כאן בפרפרזה.

הבה נניח שלחלקיק תת-אטומי (נאמר, אלקטרון) יש תכונה שנקרא לה “צבע” (זה יכול להיות הספין של אלקטרון, או הקיטוב של פוטון, וכו’). מה שלא נתכוון ב”צבע”, זוהי תכונה בינארית שיש לה רק שני ערכים – שחור ולבן. אנחנו יכולים לבנות תיבת צבע שיש לה שלושה פתחים: אחד להכנסת כל האלקטרונים (כלומר, שני הסוגים), אחד להוצאת אלקטרונים שחורים, ואחד להוצאת אלקטרונים לבנים. תיבת הצבע אינה משנה את צבע החלקיקים הנכנסים אליה. אם נשלח לתוכה אלקטרון לבן בודד, הוא תמיד (100% מהזמן) יצא דרך הפתח הלבן, וכך גם אם נשלח אלקטרון שחור בודד, הוא תמיד יצא דרך הפתח השחור. הדבר היחיד שתיבת הצבע עושה הוא לבדוק את צבע האלקטרונים ולמיין אותם בהתאם. זהו מכשיר למיון צבעים, לא יותר.

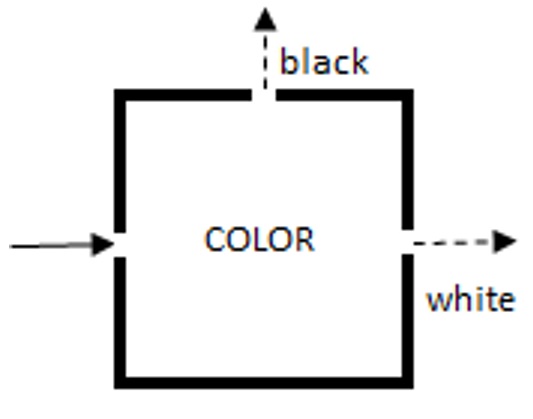
אם נערבב כמה אלקטרונים שחורים עם כמה אלקטרונים לבנים ונשלח את כולם דרך פתח הכניסה בצד שמאל של התיבה כפי שמוצג באיור 1, כל האלקטרונים השחורים יצאו דרך הפתח השחור בחלק העליון של התיבה, וכל האלקטרונים הלבנים יצאו דרך הפתח הלבן בצד ימין.

הבה נניח שלחלקיק (נאמר, אלקטרון) יש גם תכונה שנקרא לה “קשיות”. כמו צבע, קשיות היא תכונה בינארית שיש לה רק שני ערכים – במקרה זה, קשה ורך. אנחנו יכולים גם לבנות תיבת קשיות שיש לה שלושה פתחים: אחד להכנסת אלקטרונים, אחד להוצאת אלקטרונים קשים, ואחד להוצאת אלקטרונים רכים.

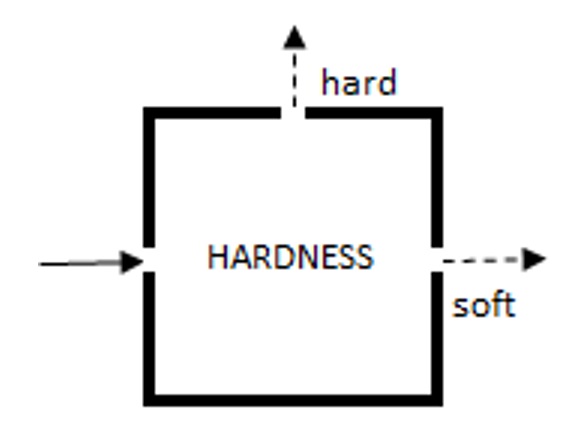
אם נערבב כמה אלקטרונים קשים ואלקטרונים רכים יחד ונשלח אותם דרך פתח הכניסה בצד שמאל, כל האלקטרונים הקשים יצאו דרך הפתח הקשה בחלק העליון של התיבה, וכל האלקטרונים הרכים יצאו דרך הפתח הרך בצד ימין, כפי שמוצג באיור 2. אנו בונים את תיבת הקושי כך שהיא לא משנה את קושי החלקיקים שנכנסים אליה. אם נשלח אלקטרון רך בודד לפתח הכניסה, הוא תמיד (100% מהזמן) יצא דרך הפתח הרך. באופן דומה, אם נשלח אלקטרון קשה בודד, הוא תמיד יצא דרך הפתח הקשה. הדבר היחיד שתיבת הקושי עושה הוא לבדוק קושי ולמיין את האלקטרונים בהתאם. זהו מכשיר למיון קושי, ותו לא.

הבה נסדר כעת שלוש תיבות בשורה: תיבת צבע, תיבת קושי, ותיבת צבע נוספת.

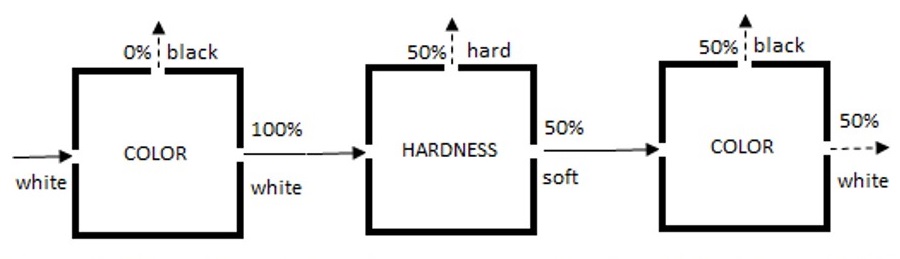
בניסוי זה, אנו שולחים רק אלקטרונים לבנים לתיבת הצבע הראשונה המוצגת בצד שמאל של איור 3. אנחנו כבר יודעים שתיבת הצבע אינה משנה את צבע החלקיקים העוברים דרכה. לכן, אנו מצפים לראות 100% מהאלקטרונים יוצאים דרך הפתח הלבן בצד ימין של תיבת הצבע. וזה בדיוק מה שקורה. האלקטרונים הלבנים היוצאים מתיבת הצבע הראשונה נכנסים כעת לתיבת הקושי במרכז איור 3. תיבת הקושי ממיינת את האלקטרונים לפי מאפיין הקושי שלהם, כאשר 50% מהאלקטרונים יוצאים דרך הפתח הקשה (אלה האלקטרונים הקשים) ו-50% יוצאים דרך הפתח הרך (אלה האלקטרונים הרכים). כעת, הבה נזין את כל האלקטרונים הרכים היוצאים מהפתח הרך לתיבת הצבע השנייה בצד ימין של איור 3. למה אנחנו מצפים לראות? באופן סביר היינו מצפים לראות את כל האלקטרונים האלה יוצאים מתיבת הצבע השנייה דרך הפתח הלבן. אכן, מכיוון ששלחנו רק אלקטרונים לבנים לתיבה האמצעית, והתיבה האמצעית לכאורה אינה עושה דבר לאלקטרונים אלה מלבד בדיקת הקושי שלהם, הצבע שלהם לא אמור – כך נראה – להיות מושפע. אבל באופן מפתיע, זה לא מה שקורה. בתיבת הצבע השנייה, חמישים אחוז מהאלקטרונים יוצאים דרך הפתח הלבן, ו-50% מהאלקטרונים יוצאים דרך הפתח השחור. משמעות הדבר היא שתיבת הצבע השנייה פגשה 50% אלקטרונים לבנים ו-50% אלקטרונים שחורים. אבל מאיפה הגיעו האלקטרונים השחורים?

תוצאה פרדוקסלית זו אומתה באינספור ניסויים, שהניבו באופן בלתי משתנה את אותה תוצאה. מסתבר שברגע שאנו מגלים מידע על קושי האלקטרונים, אנו מוחקים את כל הידע על מאפייני הצבע שלהם. למרות שהתחלנו בידיעה ש-100% מהאלקטרונים שנכנסו לתיבת הצבע הראשונה היו לבנים, לאחר מדידת קושי האלקטרונים בתיבת הקושי, מידע זה אובד, מה שאומר שיש הסתברות שווה למצוא באקראי אלקטרון לבן או שחור בסוף תהליך שלוש התיבות. זה לא שהאלקטרונים הם “בעצם” לבנים, אבל תיבת הקושי משנה את הצבע של חלק מהאלקטרונים – זה לא המקרה. תיבת הקושי אינה משנה את הצבע, אך בתהליך מדידת קושי האלקטרונים תיבת הקושי מוחקת כל מידע על צבעם, מה שאומר שיש לנו הסתברות שווה למצוא צבע לבן או שחור. (זכרו שמכניקת הקוונטים היא תיאוריה אפיסטמית – היא לא עוסקת במה שהמציאות היא, אלא במה שאנחנו יודעים על המציאות.)

במילים אחרות, האלקטרונים, שמאפיין הקשיות שלהם ידוע לנו במדויק, נמצאים במצב של סופרפוזיציה מבחינת מאפיין הצבע שלהם: הצבע שלהם אינו שחור ולא לבן ולא שניהם ולא אף אחד מהם, אלא נמצא במצב של סופרפוזיציה של צבע שחור וצבע לבן – המצב החמישי הבלתי ידוע לפיזיקה הקלאסית (ניוטונית). ניסוי מחשבתי זה, אם כן, ממחיש את מושג הסופרפוזיציה של מצבים. בעוד שבפיזיקה קלאסית, מערכת יכולה להיות רק במצב אחד בכל רגע נתון, במכניקת הקוונטים, המערכת יכולה להיות בסופרפוזיציה של מצבים. לדוגמה, אם נסובב סביבון חנוכה, הוא יסתובב בכיוון השעון או נגד כיוון השעון, בהתאם לכיוון שבו סובבנו אותו. במכניקת הקוונטים, סביבון יכול להיות בסופרפוזיציה של מצבים של סיבוב בכיוון השעון ונגד כיוון השעון. למעשה, פיזיקאים מציבים באופן שגרתי אלקטרונים בסופרפוזיציה של מצבים של ספין למעלה וספין למטה, שהוא בקירוב שווה ערך לסיבוב בכיוון השעון ונגד כיוון השעון.

ניסוי זה גם ממחיש את עקרון אי-הוודאות של הייזנברג, שלפיו, כפי שאמרנו לעיל, מצב שבו לאחד משני המאפיינים המשלימים יש ערך מוגדר מתאים איכשהו לסופרפוזיציה של מצבים רבים עבור המאפיין האחר, ובכך הופך אותו לבלתי מוגדר.

זה בדיוק מה שקורה בנרטיב התורני של עץ הדעת! כפי שהוזכר לעיל, בפיזיקת הקוונטים “צבע” ו”קושי” הם רק מחזיקי מקום לכל מאפיינים משלימים (בשפה מתמטית, “מצומדים קנונית”). ביישום מושג זה לנרטיב התורני, הבה נחליף “צבע” באמת האובייקטיבית המוחלטת על נכון ולא נכון כך שצבעים לבן ושחור מייצגים נכון ולא נכון, בהתאמה. באופן דומה, הבה נחליף “קושי” ב”טוב” כך שקשה ורך מתאימים לטוב ורע בהתאמה.

כל עוד אדם וחוה היו מחוננים ביכולת האינטלקטואלית לדעת נכון ולא נכון במדויק, הידע המשלים של טוב ורע היה במצב של סופרפוזיציה – בני האדם הראשונים, לפני חטאם הקדמון, היו אמביוולנטיים לגבי טוב ורע. לאחר החטא, המצב התהפך, כמו בדוגמה שלנו עם שלוש התיבות לעיל: הידע של טוב ורע שבא עם פרי האיסור הכניס את הידע של נכון ולא נכון למצב של סופרפוזיציה. כך, אדם וחוה לא יכלו עוד להבחין בין אמת לשקר, בין נכון ללא נכון – ועם חוסר יכולת זה בא אובדן גן העדן. כפי שאנו רואים, עץ הדעת טוב ורע שימש כתיבת ה”קושי”, כביכול, במערך שלוש התיבות לעיל, מוחק את המידע על אמת ושקר ממוחם של אדם וחוה. עץ הדעת פעל אפוא כמוחק קוונטי. (לקוראים בעלי נטייה מתמטית וקוראים המכירים מכניקת קוונטים לפחות ברמה מבואית, ראו את התוספת לפרק זה לטיפול המתמטי ברעיונות אלה.)

האגו ואובדן גן העדן

היכולת להבחין בין אמת לשקר, לדעת נכון מלא נכון, היא עניין של שיפוט. זהו שיפוט אינטלקטואלי, שאינו דורש ואכן אינו מאפשר כל מעורבות רגשית. שופט חייב להיות עצמאי וללא אינטרס אישי בעניין הנדון. כך, האגו של האדם אינו יכול להיות מעורב בתהליך. הבעיה היא שברגע שהאגו מתערב, הוא נוטה להכניס את עצמו לכל היבט בחיי האדם או במחשבותיו. כשיש אגו, אדם כבר לא יכול להחליט באופן אובייקטיבי בין נכון ללא נכון, כי קבלת ההחלטות שלו מוכתמת במעורבות הרגשית ובמודעות העצמית שלו, באגו שלו.

הידע של טוב ורע, מצד שני, הוא בדיוק ההפך מהידע של אמת ושקר – הוא דורש רגשות ואגו. בניגוד לאמת ושקר, שהם קטגוריות אובייקטיביות ומוחלטות, טוב ורע הם תמיד יחסיים לאדם השופט – האם זה טוב בשבילי? האגו קובע את נקודת ההתייחסות, שביחס אליה נקבעים טוב ורע. מעורבות האגו הנדרשת לידיעת טוב ורע מונעת את האובייקטיביות הנדרשת לידיעת נכון ולא נכון – ומכאן אי-התאימות ההדדית. מנקודת מבט זו, גן העדן הוא מטאפורה למצב התודעתי שבו מתמקדים בנכון ולא נכון אובייקטיבי במקום בטוב ורע סובייקטיבי. השינוי בפרספקטיבה מהאמת והשקר המופשטים לרגשי האם זה טוב בשבילי, או האם זה רע בשבילי הוא שינוי פרדיגמה בתודעה האנושית בממדים קוסמיים – סוף עידן התמימות.

לאחר החטא הקדמון של אדם וחוה, לכל בני האדם יש אגו,^[6] וכולנו חסרים את היכולת האינטלקטואלית לשפוט נכון ולא נכון באופן אובייקטיבי. אם הבהירות שלפני החטא נקראה גן עדן, אחרי החטא, גן העדן אבד.

מעניין לציין שבכל המסורות הרוחניות, הדרך להארה רוחנית ואיחוד עם האלוהי (unio mystica או, בעברית, דבקות^[7]) עוברת דרך תרגול הסגפנות. אנשים המחפשים כבוד, כוח, או תענוג בסיסי חולף דרך סיפוקים מיניים או חושיים אחרים אין להם תקווה להשיג הארה רוחנית, הנתפסת כבלתי תואמת לכל צורה של סיפוק עצמי.

בפירושו לפסוק “והסירותי מחלה מקרבך” (שמות כג:כה), אומר הרבי מליובאוויטש, רבי מנחם מנדל שניאורסון,

המחלה המוזכרת כאן… מתייחסת למקור כל המחלות, כלומר, לתחושת המודעות העצמית שנגרמה מחטא עץ הדעת. לפני החטא, לא היה מושג של מודעות עצמית, כפי שמשתקף בפסוק: “ויהיו שניהם ערומים ולא יתבוששו.”^[8] החטא הוביל לתחושת המודעות העצמית, כפי שמשתקף בפסוק: “ותרא האשה כי טוב העץ למאכל.”^[9] … חטא עץ הדעת השפיע על כולם, אפילו על הצדיקים.^[10]

שיעורים בספר המאמרים, מאמרים נבחרים של הרבי מליובאוויטש

הרבי מדבר עוד על ארבעה אנשים הנדונים בתלמוד^[11] שמתו לא בגלל חטאיהם, אלא בגלל “עצת הנחש”. הנחש הקדמוני הזריק את הארס של האגוצנטריות שלו לכל האנושות, ואפילו לטובים שבטובים יש מנה זעירה של אותו ארס – המודעות העצמית הנובעת מהאגו של האדם. אפילו אנשים צדיקים לחלוטין, המקדישים את עצמם ללא אנוכיות לעבודת ה’, עדיין יש להם טיפה, קטנה ככל שתהיה, של אותו ארס מהנחש הקדמוני. זה הפך לחלק מה-DNA הרוחני והפסיכולוגי שלנו.

כעת, אולי, אנחנו יכולים גם להבין מדוע האיסור על אכילת פרי עץ הדעת נשא איום בעונש כה חמור – מוות. לפני החטא הזה, בני האדם היו אמורים לחיות לנצח; לא היה אגו מנופח המשתוקק לסיפוק עצמי ולכן לא היה צורך במוות. הרוע הזה היה טמון בפרי עץ הדעת והיה, לפיכך, חיצוני לכל אדם. עם טעימת הפרי האסור והפנמת הרוע, בני האדם הראשונים ניפחו את האגו שלהם ורכשו את התשוקה האגואיסטית לסיפוק עצמי. זה, אולי, הביא לצורך במוות כאמצעי לתיקון האגו האנושי, כי המוות הוא הביטול העצמי (בעברית, ביטול) המוחלט.

הגאולה המשיחית, המרמזת במובנים רבים חזרה לעידן התמים של גן העדן שלפני החטא, נתפסת כשלב בהיסטוריה האנושית לאחר שהחטא הקדמון כופר, והאגו האנושי תוקן עד לנקודה שאינו דורש ביטול נוסף, מה שאוטומטית מסיר את המוות מהעולם. הזמן המשיחי, לפיכך, הוא שלב גן העדן כאשר נחזור למצב של הארה אינטלקטואלית כאשר נדע שוב נכון ולא נכון, אך לא נדע טוב ורע. נראה שעקרון אי-הוודאות יחזיק מעמד גם בימות המשיח.

נספח: סופרפוזיציה של מצבים

במכניקת הקוונטים, כל מצב פיזי מתואר כווקטור במרחב הילברט. מרחב הילברט הוא מרחב מופשט שהוא הרחבה של המרחב האוקלידי המוכר בכל מספר ממדים, כולל מרחב אינסופי-ממדים. וקטור הוא אובייקט מתמטי בעל כיוון וגודל, כמו חץ. במכניקת הקוונטים, מקובל לכתוב וקטורים באמצעות סימוני בראקט של דיראק, שבהם בראים וקטים מסומנים על ידי שילוב של קו אנכי | וסוגר זוויתי 〉. וקטור ברא A מסומן כ-⟨A|, ווקטור קט A מסומן כ-|A〉. הכפלת וקטור בסקלר (מספר) רק מרחיבה את גודל הוקטור מבלי לשנות את כיוונו: a|A〉 זהה ל-|aA〉.

הבה נתבונן כעת במערכת המאופיינת על ידי מצב הנקרא “אמת”. למצב האמת יש שני ערכים: אמת ושקר. לכן, שני הערכים האפשריים שלו מגדירים וקטורים במרחב הילברט דו-ממדי: |אמת〉 או |שקר〉. וקטורים אלה יכולים להיות מבוטאים כעמודות:

באלגברה לינארית, עמודה כזו נקראת גם מטריצת עמודה יחידה או וקטור. אופרטור הוא הוראה אשר, בפעולתה על וקטור במרחב הילברט, מתמירה וקטור זה לווקטור אחר באותו מרחב הילברט. לדוגמה, אם |A〉 הוא וקטור במרחב הילברט H, ו-O הוא אופרטור, O|A〉 = |A‘〉, כאשר |A‘〉 הוא וקטור אחר ב-H. אם לאופרטור O ולווקטור |A〉 יש יחס כזה ש-

כאשר a הוא מספר כלשהו, |A〉 נקרא וקטור עצמי של O, ו-a הוא ערך עצמי של O. יחס זה, כמובן, פשוט אומר שאורך הווקטור |A〉 מוארך בגורם של a מבלי לשנות את כיוונו.

אנו יכולים להגדיר אופרטור אמת T כמטריצה,

כאשר אנו מסכימים ש-“אמת = 1” פירושו “אמת” ו-“אמת = -1” פירושו “שקר”.

הבה נזכור מאלגברה לינארית את הכלל להכפלת מטריצה 2×2 במטריצת עמודה יחידה (וקטור):

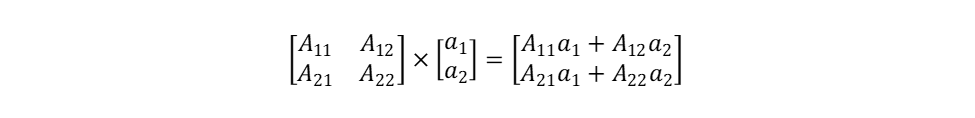
הבה נחיל כעת את אופרטור האמת על הווקטור |אמת〉:

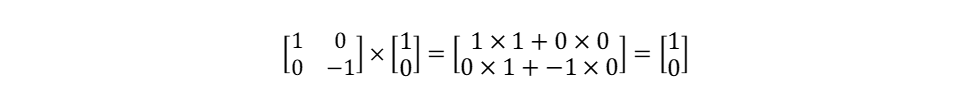
לכן, יש לנו,

T|אמת〉=1|אמת〉

כך, הוכחנו שהווקטור |אמת〉 הוא וקטור עצמי של אופרטור האמת T, ואמת (זכרו שאמת = 1) הוא ערך עצמי של אופרטור האמת T.

למערכת שהגדרנו לעיל כבעלת מצב של אמת יש מצב נוסף – “טוב”. למצב ה”טוב” יש גם שני ערכים: טוב ורע (או רע). לכן אנו יכולים להגדיר ערכים אלה כווקטורים באותו מרחב הילברט דו-ממדי: |טוב〉 ו-|רע〉. במכניקת הקוונטים, מרחב הילברט הדו-ממדי נקרא מרחב הספין (כי גם לספין יש שני ערכים – למעלה ולמטה). וקטורים אלה יכולים גם כן להיות מבוטאים כעמודות:

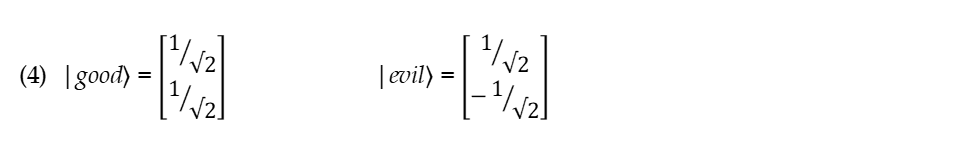
באופן דומה, הבה נגדיר אופרטור טוב G כמטריצה,

כאשר אנו מסכימים ש-“טוב = 1″ פירושו “טוב” ו-“טוב = -1″ פירושו “רע”.

קל לראות שהווקטורים |טוב〉 ו-|רע〉 הם וקטורים עצמיים של אופרטור הטוב.

הווקטורים |אמת〉, |שקר〉, |טוב〉, ו-|רע〉 נקראים וקטורי מצב כי הם מגדירים את המצב (אוסף התכונות) של המערכת הנדונה.

הבה נזכור מאלגברת וקטורים שאם לווקטור A יש רכיבים a₁ ו-a₂, ולווקטור B יש רכיבים b₁ ו-b₂:

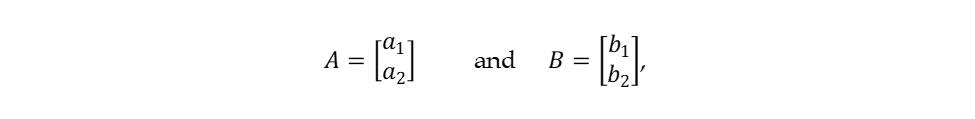
אז

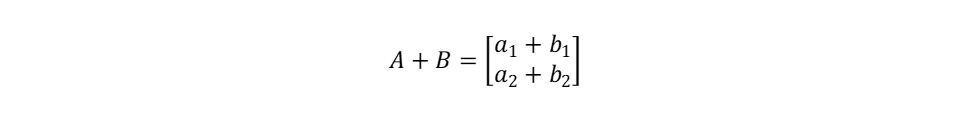
כלל נוסף מאלגברת וקטורים אומר שכדי להכפיל וקטור במספר עליך להכפיל את רכיבי הווקטור במספר זה:

נובע מ-(1) ו-(4) ש-

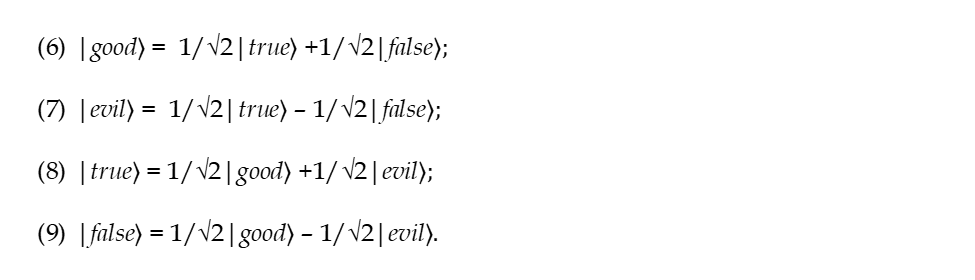
הבה נבדוק לדוגמה את השוויון הראשון. כדי לעשות זאת, הבה נחשב את הצד הימני של הביטוי (6):

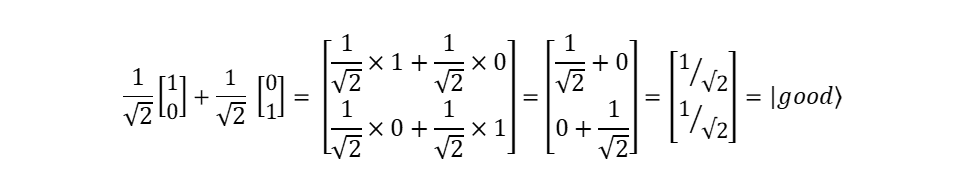
אנו רואים שהשוויון (6) אכן נכון. קל באותה מידה לאמת את נכונות השוויונות (7)-(9).

כדי לתרגם נוסחאות אלה למילים:

נוסחאות אלה מבטאות את הסופרפוזיציה של מצבים, המאשרת את עקרון אי-הוודאות של הייזנברג, הקובע שידיעת הערך המדויק של תכונה אחת מציבה את התכונה המשלימה במצב של סופרפוזיציה. כדי לראות כיצד נוסחאות אלה מבטאות מתמטית את המכניקה של החטא הקדמון של עץ הדעת, הבה נפרק את משמעותן.

הבה נתבונן במשוואות (6) ו-(7), המשוות את וקטורי המצב |טוב〉 ו-|רע〉 לקומבינציות לינאריות של וקטורי המצב של |אמת〉 ו-|שקר〉. קומבינציה לינארית של וקטורים אלה פירושה שהמערכת נמצאת במצב של סופרפוזיציה של אמת ושקר. שתי משוואות אלה אומרות שבכל פעם שמצב הטוב מוגדר היטב, כלומר, אנו יודעים בדיוק כיצד נראים וקטורי המצב |טוב〉 ו-|רע〉, מצב האמת אינו מוגדר כלל, שכן הוא מתאים למצבים של סופרפוזיציה של |אמת〉 ו-|שקר〉, כפי שמוצג במשוואות (6) ו-(7). במונחים מתמטיים, זה מתבטא בעובדה שבעוד שהווקטורים |אמת〉 ו-|שקר〉 הם וקטורים עצמיים של אופרטור האמת T, הווקטורים |טוב〉 ו-|רע〉 אינם כאלה.

בואו נבחן כעת את משוואות (8) ו-(9), המשוות את וקטורי המצב |אמת〉 ו-|שקר〉 לצירופים ליניאריים של וקטורי המצב |טוב〉 ו-|רע〉. שתי המשוואות הללו אומרות שבכל פעם שמצב האמת מוגדר היטב, כלומר אנו יודעים בדיוק איך נראים וקטורי המצב |אמת〉 ו-|שקר〉, מצב הטוב אינו מוגדר כלל, שכן הוא מתאים למצבי הסופרפוזיציה של |טוב〉 ו-|רע〉, על פי משוואות (6) ו-(7). שוב, במונחים מתמטיים, זה מתבטא בעובדה שבעוד וקטורי |טוב〉 ו-|רע〉 הם וקטורים עצמיים של אופרטור הטוב G, וקטורי |אמת〉 ו-|שקר〉 אינם כאלה.

אנו רואים, אפוא, שמצבי אמת ו-שקר מצד אחד אינם תואמים למצבי טוב ו-רע מצד שני—בכל פעם שיש לנו מצב מוגדר של אמת או שקר, יש לנו סופרפוזיציה של מצבי טוב ו-רע, ולהיפך.

מצב זה דומה בדיוק למצבי המנטליות של אדם וחוה בגן עדן לפני החטא ואחריו. לפני שטעמו מעץ הדעת טוב ורע, הם ידעו בדיוק מה אמת ומה שקר; הם ידעו להבחין בין נכון לשגוי. האגו שלהם לא הכתים את שיפוטם, ובהיותם חופשיים מכל רצונות אגואיסטיים לסיפוק עצמי, לא היה להם מושג של טוב ורע, שעבורם התקיימו במצב מופשט של סופרפוזיציה.

אולם לאחר שטעמו מהפרי האסור, המצב התהפך. לאחר שניפחו את האגו שלהם ורכשו את הטעם של סיפוק עצמי, הם רכשו את הידיעה של טוב (מה שטוב עבורי) ורע (מה שרע עבורי). כתוצאה מכך, כפי שקובע הרמב”ם במורה נבוכים, הם איבדו את כל הידיעה של אמת ושקר, שעברה מהיותה מוגדרת היטב לפני החטא הקדמון למצב מופשט של סופרפוזיציה לאחר החטא. המידע על אמת ושקר נמחק על ידי הפרי האסור של עץ הדעת—המוחק הקוונטי. אדם וחוה איבדו את יכולתם לשפוט באופן אובייקטיבי בין נכון לשגוי.

מטמורפוזה זו מאושרת על ידי משוואות (6)-(9).

אנו רואים מהאמור לעיל שההקבלות שלנו בין עקרון האי-ודאות של הייזנברג לחטא הקדמון על פי הרמב”ם, בין הקשר של נכון ושגוי, וטוב ורע לסופרפוזיציה של מצבים, בין הפרי האסור למוחק קוונטי אינן רק מילים אלא מייצגות הקבלות מבניות מדויקות שניתן לתאר בקלות מתמטית. אפשר רק להתפעל מהעובדה הבלתי ניתנת להכחשה שמושגים מוזרים אלה של פיזיקה קוונטית מקודדים בנרטיב המקראי.

הערות שוליים:

[1] הרב משה בן מימון (הידוע גם כ-רמב”ם) (1138/1135–1204), הפילוסוף והמקודד היהודי הבולט ביותר מימי הביניים, שתפקידו החריג ביהדות בא לידי ביטוי בכתובת על מצבתו: “ממשה עד משה לא קם כמשה”.

[2] אני אסיר תודה לחתני, מימון קירשנבאום, על שהביא הקבלה זו לתשומת ליבי.

[3] בפיזיקה, זוגות משתנים כאלה נקראים משתנים מצומדים קנונית; דוגמאות לזיווגים כאלה כוללים קואורדינטות ותנע, או זמן ואנרגיה.

[4] עקרון האי-ודאות של הייזנברג קובע: Δx×Δp ≥ ½ћ, כאשר Δx הוא האי-ודאות במדידת המיקום x, Δp הוא האי-ודאות במדידת התנע p, ו-ћ הוא קבוע פלאנק המופחת h/2π.

[5] ראה פרק 1 של דיוויד ז. אלברט, “מכניקה קוונטית וחוויה” (הוצאת אוניברסיטת הרווארד, 1992).

[6] השימוש הידוע הראשון במילה “אגו” במשמעות העצמי/תודעת העצמי היה בשנת 1789, על ידי יוהאן גוטליב פיכטה, פילוסוף אידיאליסט גרמני. אולם לא פיכטה ולא פרויד, שעמו המילה הזו מזוהה בעיקר, המציאו את האגו; הם היו הראשונים לדבר עליו בפילוסופיה ובפסיכיאטריה המודרנית. המילים יש (“עצמי”) או ישות (“אגו”, “עצמיות”) שימשו גם הן באופן נרחב במחשבה היהודית ובמיוחד בפילוסופיה החסידית.

[7] המושג הקבלי של דבקות, מצב אקסטטי של “דבקות” באלוהים, אינו זהה למושג של unio mystica, שבמסורות רוחניות אחרות משמעותו התמזגות עם האלוהי. ביהדות, נשמה אנושית אינה יכולה להתאחד לחלוטין עם אלוהים, שנשאר לחלוטין טרנסצנדנטי ובלתי ניתן להכרה. הטוב ביותר שאנחנו יכולים לעשות הוא לשאוף לדבוק באלוהים על ידי ביטול האגו שלנו—ביטול.

[8] בראשית ב:כה

[9] בראשית ג:ו

[10] שיעורים בספר המאמרים, מבחר מאמרים של הרבי מליובאוויטש, “לא תהיה משכלה” (ניו יורק: הוצאת קה”ת, 2015), עמ’ 168–173.

[11] תלמוד, מסכת שבת, נה ע”ב; מסכת בבא בתרא יז ע”א.