ה-14 במרץ נחגג על ידי חובבי מדע בכל העולם כיום הפאי. כאשר כותבים בספרות, 3/14 מייצג את שלוש הספרות הראשונות של המספר המיוצג באופן מסורתי על ידי האות היוונית “π” (מבוטא פאי) – 3.14. יום הפאי נחגג על ידי אכילת פאי ודיון בחשיבות של π. אנשים מסוימים שיש להם יותר מדי זמן פנוי מתחרים בשינון הספרות העשרוניות המייצגות את ערך הפאי. השיא כרגע עומד על 67,890 ספרות! בעוד שאכילת פאי היא אופציונלית, דיון בחשיבות של π הוא באמת חובה.
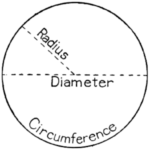
אז, מהו π ומדוע הוא כל כך חשוב? π הוא ללא ספק הקבוע המתמטי המפורסם ביותר, המבטא את היחס בין היקף המעגל לקוטרו. אם תיקח מעגל בקוטר של 1, היקף המעגל הזה ימדוד בקירוב 3.14159265… – כאשר “בקירוב” היא המילה המפתח כאן, אבל עוד על כך בהמשך. לכן, עבור מעגל ברדיוס (חצי מהקוטר) “r”, היקף המעגל נמדד כ-2πr, ושטח המעגל מחושב כ-πr2. אפשר לראות מדוע π כל כך חשוב במדידת קרקע, למשל.
עם זאת, π מופיע לא רק בגיאומטריה, אלא גם בתורת המספרים, אלגברה, אנליזה, סטטיסטיקה ותחומים מתמטיים אחרים. בפיזיקה, π הוא באמת נמצא בכל מקום.
בעת העתיקה, הבבלים קירבו את π למספר השלם הקרוב ביותר – 3. עם זאת, מדידת קרקע, אדריכלות והנדסה דורשות כולן ידע של π בדיוק סביר. הבבלים ידעו שהמספר השלם 3 היה רק קירוב גס.

לוח בבלי שנמצא ליד סוזה (מהמאות ה-19 עד ה-17 לפנה”ס) נותן קירוב של π כ-25⁄8 = 3.125, מקבל את הספרה העשרונית הראשונה נכון.

פפירוס רינד המצרי (בסביבות 1600 לפנה”ס) מקרב את π ל-256⁄81 ≈ 3.16. חלק מהמצרולוגים טוענים שבוני הפירמידות השתמשו ביחס 22⁄7 = 3.142… עבור π. כמובן, שתי הספרות העשרוניות הראשונות בקירוב זה נכונות. בשטפטה ברהמנה (בסביבות המאה ה-6 לפנה”ס), אסטרונומים הודים העריכו את π כ-339/108 = 3.139…

במאה ה-3 לפנה”ס, ארכימדס הוכיח ש-π גדול מ-223⁄71 ≈ 3.1408…, אך קטן מ-22⁄7 ≈ 3.1428… במאה ה-2 לפנה”ס, האסטרונום היווני תלמי השתמש בקירוב של 377⁄120 ≈ 3.1416… במאה ה-3 לספירה, המתמטיקאי הסיני ליו הוי קירב את π בדיוק רב לארבע ספרות עשרוניות כ-3927/1250 = 3.1416. במאה ה-6 לספירה, מתמטיקאים הודים קיבלו את אותו ערך של π כ-62832/20000 = 3.1416. עד המאה ה-5 לספירה, מתמטיקאים סינים שיפרו את ערך π עד לספרה השביעית. כיום, ערך π ידוע לטריליוני ספרות.

הערך המדויק של π התגלה לראשונה על ידי המתמטיקאי הגרמני גוטפריד לייבניץ. הנוסחה של לייבניץ ל-π היא סדרה אינסופית:
העובדה שהערך המדויק של π יכול להיות מבוטא רק כסדרה אינסופית היא משמעותית מאוד, כפי שנראה בהמשך.
היהודים שיצאו ממצרים בוודאי היו מודעים לערך המקורב של π שהיה בשימוש אז על ידי המצרים – אחרי הכל, עבדים יהודים בנו את הפירמידות. לכן, חלק מעלים שאלה, מדוע התנ”ך נותן את הקירוב הגס ביותר של π. אכן, במלכים א’ ז:כג אנו קוראים:
וַיַּעַשׂ אֶת־הַיָּם מוּצָק עֶשֶׂר בָּאַמָּה מִשְּׂפָתוֹ עַד־שְׂפָתוֹ עָגֹל סָבִיב וְחָמֵשׁ בָּאַמָּה קוֹמָתוֹ וקוה [וְקָו] שְׁלֹשִׁים בָּאַמָּה יָסֹב אֹתוֹ סָבִיב׃
באופן דומה, בדברי הימים ב’ ד:ב אנו מוצאים קטע כמעט זהה:
וַיַּעַשׂ אֶת־הַיָּם מוּצָק עֶשֶׂר בָּאַמָּה מִשְּׂפָתוֹ אֶל־שְׂפָתוֹ עָגוֹל סָבִיב וְחָמֵשׁ בָּאַמָּה קוֹמָתוֹ וְקָו שְׁלֹשִׁים בָּאַמָּה יָסֹב אֹתוֹ סָבִיב׃
האגן העגול העשוי ממתכת יצוקה עבור בית המקדש (הראשון) בירושלים על ידי המלך שלמה היה בקוטר של 10 אמות והיקף של 30 אמות. בהתאם לכך, נראה כי π מרומז להיות 3. בית המקדש הראשון נבנה על ידי המלך שלמה בשנת 832 לפנה”ס. עד אז, הבבלים והמצרים כבר ידעו טוב יותר מזה.
גם אם נניח, לצורך הטיעון, שהעברים הקדמונים לא ידעו את ערך π מעבר לערכו השלם (3), הם בוודאי ידעו כיצד למדוד. אם הם עשו את האגן בקוטר של 10 אמות, כאשר הם מדדו את היקפו, הם היו מוצאים שהוא בערך 31.41 אמות; עיגול למספר השלם הקרוב ביותר היה מביא לתוצאה של 31 אמות, לא 30. הרבי מלובביץ’, הרב מנחם מנדל שניאורסון, הסביר זאת כך: ההיקף של האגן היה למעשה 30 אמות. בהתאם לכך, הקוטר היה בערך 9.55 אמות ועוגל כלפי מעלה למספר השלם 10. הסבר זה פותר את השאלה מדוע ההיקף היה 30 אמות ולא 31.
למעשה, אני לא רואה בעיה כאן בכלל. התנ”ך אינו ספר לימוד במתמטיקה. בשום מקום בפסוקים המצוטטים הנביאים לא מתיימרים לגלות לנו את ערך π. הפסוקים מתארים את מידות האגן ששימש במקדש. כפי שהרבי הסביר, בהינתן היקף האגן של 30 אמות, הקוטר יצא קצת פחות מ-10 אמות ופשוט עוגל ל-10. האגן כבר נבנה, כך שלא היה צורך בשרטוטים הנדסיים מדויקים או מידות מדויקות. הכתוב פשוט מודיע לנו על מידות מקורבות של האגן, שמעוגלות למספרים שלמים. אין בכך שום דבר מוזר או יוצא דופן.
עם זאת, חלק מחכמינו חשבו שהפסוקים המצוטטים לעיל דרשו הסבר. כך, משנת המידות מנסה לפתור בעיה זו על ידי הנחת שפה בעובי של כ-0.225 אמות, שנכללה במדידת הקוטר, אך לא בהיקף. כך, היא מקרבת את π ל-22⁄7, או 3.14135… עם זאת, תיארוך מקור זה אינו ברור. יש המייחסים אותו לתנא, רבי נחמיה, ובמקרה זה ניתן לתארך עבודה זו לסביבות 150 לספירה, בעוד שרשויות אחרות מתארכות ספר זה לתקופה הגאונית המאוחרת, סביב המאה ה-9 לספירה.
בקפיצה קדימה למאה העשרים, הרב מקס מונק הציע תובנה מעניינת על הפסוקים בתנ”ך. (תובנה זו מיוחסת לעתים קרובות בטעות לגר”א. דבר זה הוכחש בתוקף על ידי פרופ’ אלישקוב וד”ר פיינס במאמר “האם המקרא והמתמטיקה חלוקים על המספר π?” ב’אור התורה’, 17, עמ’ 141-42.)
במלכים א’, המילה הכתובה (כתיב) המשמשת ל”קוטר” היא “קוה” (קוף-וו-הא), שאין לה משמעות בהקשר זה. לעומת זאת, בדברי הימים ב’, המילה לקוטר מאויתת כ”קָו” (קוף-וו), שמשמעותה “קו”. אולם, על פי המסורה (המסורת המסורתית), המילה במלכים א’ נקראת אחרת מכפי שהיא כתובה (קרי)—היא נקראת כקָו (קוף-וו), בדיוק כפי שכתוב בדברי הימים ב’. הרב מונק מציין שהגימטריה של קוה (100+6+5) היא 111 והגימטריה של קו (100+6) היא 106. הוא פירש את היחס בין שני ערכים אלה – 111/106 – כגורם תיקון: אם מכפילים את הערך המשתמע של π (3) בגורם זה, מקבלים 333/106 = 3.14150… – קירוב של π המדויק עד לנקודה העשרונית הרביעית. זה היה קירוב הרבה יותר מדויק של π ממה שהיה ידוע במשך מאות שנים לאחר מכן.
בסופו של דבר, לא משנה איזה יחס תמצאו, הוא תמיד יהיה רק קירוב לערך האמיתי של π ולכן תמיד יהיה פתוח לביקורת.

הבעיה האמיתית היא ש-π לעולם לא יכול להיות מבוטא באמת כיחס בין שני מספרים שלמים – הוא מספר אי-רציונלי (מספרים רציונליים הם אלה שניתן לבטא כיחס בין שני מספרים שלמים). מעניין לציין שהרמב”ם היה הראשון שטען ש-π הוא אי-רציונלי. בהסברו למשנה המניחה 3 כערך ההלכתי של π, מסביר הרמב”ם שהמספר 3 הוא קירוב טוב כמו כל קירוב אחר, מכיוון שאיננו יכולים לחשב את π במדויק בכל מקרה. מלבד היותו מספר אי-רציונלי, π הוא גם מספר טרנסצנדנטי, כלומר הוא אינו פתרון או שורש של משוואה אלגברית.

פעם שאלתי את הרב עדין שטיינזלץ (שיהיה לו רפואה שלמה), אם מספרים אי-רציונליים וטרנסצנדנטיים הם אמיתיים, היכן ניתן למצוא אותם בתורה?” בתגובה, הרב שטיינזלץ ציטט אמירה מפורסמת של המתמטיקאי היהודי-גרמני בן המאה ה-19 ליאופולד קרונקר, שאמר: “Die ganzen Zahlen hat der liebe G-tt gemacht, alles andere ist Menschenwerk” (א-לוהים ברא את המספרים השלמים, כל השאר הוא מעשה ידי אדם).
זו אינה שאלה טריוויאלית. למעשה, זהו לב הוויכוח בפילוסופיה של המתמטיקה האם אובייקטים מתמטיים “קיימים” במובן האונטולוגי ו”מתגלים” על ידי מתמטיקאים, או שהם “הומצאו” על ידי מתמטיקאים וקיימים רק בתודעתנו. אפלטון ייסד את אסכולת המחשבה שאובייקטים מתמטיים קיימים כצורות אידיאליות ומתגלים על ידינו. קרונקר, לעומת זאת, החזיק בדעה ההפוכה. נראה לי שבבחירת מספר שלם (3) שהוא קירוב גס של π, הנביאים לא הפגינו בורות לגבי קירובים טובים יותר שהיו ידועים בעת העתיקה; במקום זאת, הם חשפו בפנינו משהו אחר – אמת עמוקה על טבע המתמטיקה. כפי שקרונקר ביטא זאת, “א-לוהים ברא את המספרים השלמים, כל השאר הוא מעשה ידי אדם.”

כפי שגיאורג קנטור הוכיח במאה ה-19, יש אינסוף יותר מספרים אי-רציונליים וטרנסצנדנטיים ממספרים רציונליים. יתר על כן, מספרים רציונליים ואי-רציונליים מייצגים שני סוגים שונים של אינסוף. מספרים שלמים (ורציונליים) ניתנים לספירה עד אינסוף, אך בכל נקודת זמן נתונה, תמיד יש מספר סופי של מספרים שספרת עד כה. מספרים רציונליים נקראים בני-מנייה. סוג זה של אינסוף נקרא אינסוף פוטנציאלי. מספרים ממשיים הכוללים מספרים אי-רציונליים וטרנסצנדנטיים הם שונים. אם תיקח קו ממשי ותסמן עליו קטע סופי, נניח בין אפס לאחד, יהיו אינסוף נקודות (כלומר, מספרים ממשיים) על קטע זה. מספרים אי-רציונליים נקראים בלתי-מנייה. אינסוף כזה נקרא האינסוף הממשי.
המדרש רבה אומר שבעת בריאת העולם, הקב”ה הסתכל בתורה כבתוכנית. אף אחד מהמספרים האלה לא נמצא בתורה. שום חישוב גימטריה לא יכול להוביל למספר אי-רציונלי או טרנסצנדנטלי, כמו π. אם הם אמיתיים, מדוע איננו מוצאים אותם בתורה – התוכנית של הבריאה? או אולי, התורה אומרת לנו שהם לא שם כי הם לא אמיתיים (ללא כוונת משחק מילים)?

השאלה לגבי השימוש במספרים ממשיים (לא כל שכן מרוכבים) הכוללים מספרים אי-רציונליים וטרנסצנדנטליים בפיזיקה היא מאוד מפוקפקת. ארנסט מאך (פילוסוף של הפיזיקה המפורסם בעקרון מאך, שהשפיע עמוקות על איינשטיין), כמו פילוסופים פוזיטיביסטים אחרים, חש שרק כמויות הניתנות למדידה פיזית צריכות להיות מותרות בתיאוריה פיזיקלית. עם זאת, בכל פעם שאנו מודדים משהו, התוצאה היא תמיד מספר שלם או מספר רציונלי, לעולם לא אי-רציונלי או טרנסצנדנטלי. אם כך, כיצד מותר לנו להשתמש במספרים אי-רציונליים וטרנסצנדנטליים בפיזיקה, אם הם אינם ניתנים לספירה? התמודדתי עם שאלה זו מאז שהייתי נער. מעולם לא מצאתי תשובה… אולי עלינו לבנות עבור הפיזיקה מתמטיקה מיוחדת המבוססת על מספרים רציונליים בלבד? זוהי אחת מהשאלות והתעלומות הרבות של המספר π.
###
(הגרסה המקוצרת של מאמר זה פורסמה היום על ידי ‘הג’ואיש פרס’)